具有数学公式的 MATLAB 中的相邻元素
Adjacent Elements in MATLAB with Mathematical Formulation
我有一个包含 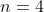 个元素的集合
个元素的集合  ,可能的相邻组合是:
,可能的相邻组合是:
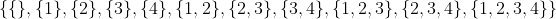
所以总共可能的组合是c=11,可以用公式计算:
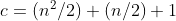
我可以使用如下所示的 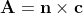 对其进行建模,其元素可以表示为 a(n,c) 是:
对其进行建模,其元素可以表示为 a(n,c) 是:
我试图在 MATLAB 中实现它,但由于我有 hard-coded 以上数学,我的代码在 n > 4:
的情况下不可扩展
n=4;
c=((n^2)/2)+(n/2)+1;
A=zeros(n,c);
for i=1:n
A(i,i+1)=1;
end
for i=1:n-1
A(i,n+i+1)=1;
A(i+1,n+i+1)=1;
end
for i=1:n-2
A(i,n+i+4)=1;
A(i+1,n+i+4)=1;
A(i+2,n+i+4)=1;
end
for i=1:n-3
A(i,n+i+6)=1;
A(i+1,n+i+6)=1;
A(i+2,n+i+6)=1;
A(i+3,n+i+6)=1;
end
是否有一个复杂度相对较低的方法来在 MATLAB 中使用 n 个元素集合 N 来转换这个问题,按照我的上述数学公式?
解决这个问题的简单方法是采用前 k 位设置的位模式并将其向下移动 n - k 次,将每个移位的列向量保存到结果中。所以,从
开始
1
0
0
0
Shift 1、2、3次得到
|1 0 0 0|
|0 1 0 0|
|0 0 1 0|
|0 0 0 1|
我们将使用 circshift 来实现这一点。
function A = adjcombs(n)
c = (n^2 + n)/2 + 1; % number of combinations
A = zeros(n,c); % preallocate output array
col_idx = 1; % skip the first (all-zero) column
curr_col = zeros(n,1); % column vector containing current combination
for elem_count = 1:n
curr_col(elem_count) = 1; % add another element to our combination
for shift_count = 0:(n - elem_count)
col_idx = col_idx + 1; % increment column index
% shift the current column and insert it at the proper index
A(:,col_idx) = circshift(curr_col, shift_count);
end
end
end
用 n = 4 and 6 调用函数我们得到:
>> A = adjcombs(4)
A =
0 1 0 0 0 1 0 0 1 0 1
0 0 1 0 0 1 1 0 1 1 1
0 0 0 1 0 0 1 1 1 1 1
0 0 0 0 1 0 0 1 0 1 1
>> A = adjcombs(6)
A =
0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1
0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 0 1 1 1
0 0 0 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 1 1
0 0 0 0 1 0 0 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1
0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 1 1 1 1
0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1 1
我有一个包含 个元素的集合
,可能的相邻组合是:
所以总共可能的组合是c=11,可以用公式计算:
我可以使用如下所示的 对其进行建模,其元素可以表示为 a(n,c) 是:
我试图在 MATLAB 中实现它,但由于我有 hard-coded 以上数学,我的代码在 n > 4:
n=4;
c=((n^2)/2)+(n/2)+1;
A=zeros(n,c);
for i=1:n
A(i,i+1)=1;
end
for i=1:n-1
A(i,n+i+1)=1;
A(i+1,n+i+1)=1;
end
for i=1:n-2
A(i,n+i+4)=1;
A(i+1,n+i+4)=1;
A(i+2,n+i+4)=1;
end
for i=1:n-3
A(i,n+i+6)=1;
A(i+1,n+i+6)=1;
A(i+2,n+i+6)=1;
A(i+3,n+i+6)=1;
end
是否有一个复杂度相对较低的方法来在 MATLAB 中使用 n 个元素集合 N 来转换这个问题,按照我的上述数学公式?
解决这个问题的简单方法是采用前 k 位设置的位模式并将其向下移动 n - k 次,将每个移位的列向量保存到结果中。所以,从
1
0
0
0
Shift 1、2、3次得到
|1 0 0 0|
|0 1 0 0|
|0 0 1 0|
|0 0 0 1|
我们将使用 circshift 来实现这一点。
function A = adjcombs(n)
c = (n^2 + n)/2 + 1; % number of combinations
A = zeros(n,c); % preallocate output array
col_idx = 1; % skip the first (all-zero) column
curr_col = zeros(n,1); % column vector containing current combination
for elem_count = 1:n
curr_col(elem_count) = 1; % add another element to our combination
for shift_count = 0:(n - elem_count)
col_idx = col_idx + 1; % increment column index
% shift the current column and insert it at the proper index
A(:,col_idx) = circshift(curr_col, shift_count);
end
end
end
用 n = 4 and 6 调用函数我们得到:
>> A = adjcombs(4)
A =
0 1 0 0 0 1 0 0 1 0 1
0 0 1 0 0 1 1 0 1 1 1
0 0 0 1 0 0 1 1 1 1 1
0 0 0 0 1 0 0 1 0 1 1
>> A = adjcombs(6)
A =
0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1
0 0 1 0 0 0 0 1 1 0 0 0 1 1 0 0 1 1 0 1 1 1
0 0 0 1 0 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1 1 1
0 0 0 0 1 0 0 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1
0 0 0 0 0 1 0 0 0 0 1 1 0 0 1 1 0 1 1 1 1 1
0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 1 1