通过不使用 pow() 的 C 程序求整数 m 的 n 次方
Finding nth power of integer m through C program without pow()
不使用 pow() 计算整数 m 的 n 次方的 C 程序。
输入:
m=3 n=2
output:
9.000
验证程序按预期工作的测试!
- 对于负M
Input : -2 3
output : -8.000
- 对于负 N
Input : 2 -3
output : 0.125000
- 对于负 M 和 N
Input : -2 -3
output : -0.125000
但是我没有得到想要的输出
void main()
{
signed int m, n;
int i;
float p;
clrscr();
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
p=1;
if (n==0)
{
printf("%d raised to %d is: %f",m,n,p);
}
if (n>0)
{
for( i = 0 ; i < n ; i++ )
p*=m;
if(m>0)
printf("%d raised to %d is: %f",m,n,p);
if(m<0)
printf("%d raised to %d is: %f",m,n,-p);
}
if (n<0)
{
n=-n;
for( i = 0 ; i < n ; i++ )
p*=m;
if(m>0)
printf("%d raised to %d is: %f",m,-n,1/p);
if(m<0)
printf("%d raised to %d is: %f",m,-n,-(1/p));
}
getch();
}
能否请您提供正确的测试用例程序?
我无法声明 signed float,因为它给出了一个错误。
否定代码不正确。当基数 m 为负数时,您不能盲目地 取反 结果。
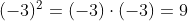 ,但
,但 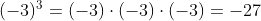 。此外,如果
。此外,如果 m 为零,则不会打印任何内容!
和 int 是默认签名的,所以 signed int 是噪音。 float 也签名了;但在这里您也可以使用 double 以获得更高的精度。 main 的 return 值应该是 int.
因此固定代码将是(根据您的喜好添加非标准 clrscrs 和 getchs ;):
#include <stdio.h>
#include <stdlib.h>
int main()
{
int m, n, i;
double p = 1.0;
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
if (n==0) {
printf("%d raised to %d is: %f",m,n,p);
}
else if (n > 0) {
for(i = 0; i < n; i++)
p*=m;
printf("%d raised to %d is: %f",m,n,p);
}
else { // n < 0
n = -n;
for (i = 0 ; i < n ; i++)
p*=m;
printf("%d raised to %d is: %f", m, -n, 1 / p);
}
}
尝试更改:
void main()
{
signed int m, n;
int i;
float p;
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
p=1;
if (n==0)
{
printf("%d raised to %d is: %f",m,n,p);
}
if (n>0)
{
for( i = 0 ; i < n ; i++ )
p*=m;
printf("%d raised to %d is: %f",m,n,p);
}
if (n<0)
{
n=-n;
for( i = 0 ; i < n ; i++ ){
p*=m;
}
printf("%d raised to %d is: %f",m,-n,1/p);
}
}
很好地识别了 OP 代码中的错误。
作为与 pow() 替代相关的面试问题,当然,采用 log2 N 步(如下所示)的解决方案优于采用 N 步(OP 的方法)的解决方案,其中 N 是指数。
关键是在每次迭代中对基数求平方。
使用 log2 N 步骤而不是 N 导致最低有效数字的错误更少。
对于负指数,简单地反转底数。
使用 double 提供至少 10 位(通常为 17 位)精度的小数位。
double powdii(int x, int y) {
double z = 1.0;
double base = x;
if (y < 0) {
base = 1.0 / base;
}
while (y != 0.0) {
if (y % 2) {
z *= base;
}
y /= 2;
base *= base;
}
return z;
}
不使用 pow() 计算整数 m 的 n 次方的 C 程序。
输入:
m=3 n=2
output:
9.000
验证程序按预期工作的测试!
- 对于负M
Input : -2 3 output : -8.000
- 对于负 N
Input : 2 -3 output : 0.125000
- 对于负 M 和 N
Input : -2 -3 output : -0.125000
但是我没有得到想要的输出
void main()
{
signed int m, n;
int i;
float p;
clrscr();
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
p=1;
if (n==0)
{
printf("%d raised to %d is: %f",m,n,p);
}
if (n>0)
{
for( i = 0 ; i < n ; i++ )
p*=m;
if(m>0)
printf("%d raised to %d is: %f",m,n,p);
if(m<0)
printf("%d raised to %d is: %f",m,n,-p);
}
if (n<0)
{
n=-n;
for( i = 0 ; i < n ; i++ )
p*=m;
if(m>0)
printf("%d raised to %d is: %f",m,-n,1/p);
if(m<0)
printf("%d raised to %d is: %f",m,-n,-(1/p));
}
getch();
}
能否请您提供正确的测试用例程序?
我无法声明 signed float,因为它给出了一个错误。
否定代码不正确。当基数 m 为负数时,您不能盲目地 取反 结果。
,但
。此外,如果
m 为零,则不会打印任何内容!
和 int 是默认签名的,所以 signed int 是噪音。 float 也签名了;但在这里您也可以使用 double 以获得更高的精度。 main 的 return 值应该是 int.
因此固定代码将是(根据您的喜好添加非标准 clrscrs 和 getchs ;):
#include <stdio.h>
#include <stdlib.h>
int main()
{
int m, n, i;
double p = 1.0;
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
if (n==0) {
printf("%d raised to %d is: %f",m,n,p);
}
else if (n > 0) {
for(i = 0; i < n; i++)
p*=m;
printf("%d raised to %d is: %f",m,n,p);
}
else { // n < 0
n = -n;
for (i = 0 ; i < n ; i++)
p*=m;
printf("%d raised to %d is: %f", m, -n, 1 / p);
}
}
尝试更改:
void main()
{
signed int m, n;
int i;
float p;
printf("Enter the number and its power (exponent)\n");
scanf("%d%d",&m,&n);
p=1;
if (n==0)
{
printf("%d raised to %d is: %f",m,n,p);
}
if (n>0)
{
for( i = 0 ; i < n ; i++ )
p*=m;
printf("%d raised to %d is: %f",m,n,p);
}
if (n<0)
{
n=-n;
for( i = 0 ; i < n ; i++ ){
p*=m;
}
printf("%d raised to %d is: %f",m,-n,1/p);
}
}
作为与 pow() 替代相关的面试问题,当然,采用 log2 N 步(如下所示)的解决方案优于采用 N 步(OP 的方法)的解决方案,其中 N 是指数。
关键是在每次迭代中对基数求平方。
使用 log2 N 步骤而不是 N 导致最低有效数字的错误更少。
对于负指数,简单地反转底数。
使用 double 提供至少 10 位(通常为 17 位)精度的小数位。
double powdii(int x, int y) {
double z = 1.0;
double base = x;
if (y < 0) {
base = 1.0 / base;
}
while (y != 0.0) {
if (y % 2) {
z *= base;
}
y /= 2;
base *= base;
}
return z;
}