Tensorflow:在同一操作中共享两个不同变量的值
Tensorflow: share value for two different variables within same operation
我最近一直在试验 TensorFlow (TF),我遇到了这个问题:假设我想计算函数的值和梯度

其中 x 的索引不同,但都指向相同的向量 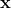 ,并且 J 是随机常数(在物理学中这是一个自旋玻璃模型)。然后
,并且 J 是随机常数(在物理学中这是一个自旋玻璃模型)。然后 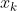 的梯度就是
的梯度就是

因此 f 对 N^3 项求和,gradf 对 N^2 项求和 N 次。我通过将总和的所有项生成为 3 阶张量并在所有条目上生成 sum-reducing 来实现 f。然后为了区分我申请
tf.gradients(f, xk)[0]
其中 f 是损失函数,xk 是变量。这是一个 MWE,假设所有 J 都是 1
import numpy as np
import tensorflow as tf
#first I define the variable
n=10 #size of x
x1 = tf.Variable(tf.zeros([n], dtype='float64'))
x2 = tf.placeholder(tf.float64, shape=[n])
#here I define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x2, [n,1])),
tf.reshape(x2, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
#run on test array
xtest = np.ones(n)
res = session.run([f, tf.gradients(f, x1)[0]],
feed_dict={x1 : xtest,
x2 : xtest})
assert res[0] == 1000
assert all(res[1] == np.array([100 for _ in xrange(n)]))
我需要独立调用 run 多次,我想将变量赋值的数量减少到只有一个,因为 x1、x2 指的是同一个向量。
n=200(在 GeForce GTX 650 上)相关示例的一些分析表明
- cuMemcpyDtoHAsync 占用 63% 的时间
- cuMemcpyHtoDAsync 18% 和
- cuEventRecord 18%。
(此 mwe 的结果相似)
因此,在 GPU 上执行计算时,分配是最昂贵的操作。显然,随着 n 的增加,开销变得更糟,因此部分抵消了使用 GPU 的好处。
关于如何通过仅传输一次 x 来减少开销的任何建议?
还有关于如何减少任何其他开销的任何其他建议将不胜感激。
编辑
为了展示实际问题,我将遵循 mrry 的建议。
如果我用 x1 替换 x2 的所有实例,那么 MWE 将如下所示
#first I define the variable
n=10 #size of x
x1 = tf.Variable(tf.zeros([n], dtype='float64'))
#here I define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x1, [n,1])),
tf.reshape(x1, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
#run on test array
xtest = np.ones(n)
session.run(x1.assign(xtest))
res = session.run([f, tf.gradients(f, x1)[0]])
assert res[0] == 1000
for g in res[1]:
assert g == 100
并且第二个断言会失败,因为梯度的每个条目都是 300 而不是 100,因为它应该是。原因是虽然 xi、xj、xk 都指代相同的向量,但它们在符号上是不同的:用相同的变量替换所有 x 将导致 x^3 的导数,即 3*x^2,因此结果第二个 MWE。
P.S。为了清楚起见,我还明确分配了 x1
实现您想要的结果的一种方法是使用 tf.stop_gradient() 操作来制作变量 x1 的有效副本,而不会影响梯度:
import numpy as np
import tensorflow as tf
# First define the variable.
n = 10 # size of x
x1 = tf.Variable(tf.zeros([n], dtype=tf.float64))
x2 = tf.stop_gradient(x1)
# Now define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x2, [n,1])),
tf.reshape(x2, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
# Run on test array
xtest = np.ones(n)
res = session.run([f, tf.gradients(f, x1)[0]],
feed_dict={x1 : xtest})
assert res[0] == 1000
for g in res[1]:
assert g == 100
我无法在上面评论(信誉不够),但请注意分析梯度应该是
$$
\frac{\partial f}{\partial x_k} = \sum_{ij} J_{ijk} x_i x_j + \sum_{ij} J_{ikj} x_i x_j + \sum_{ij} J_{kij} x_i x_j。
$$
我最近一直在试验 TensorFlow (TF),我遇到了这个问题:假设我想计算函数的值和梯度
其中 x 的索引不同,但都指向相同的向量 ,并且 J 是随机常数(在物理学中这是一个自旋玻璃模型)。然后
的梯度就是
因此 f 对 N^3 项求和,gradf 对 N^2 项求和 N 次。我通过将总和的所有项生成为 3 阶张量并在所有条目上生成 sum-reducing 来实现 f。然后为了区分我申请
tf.gradients(f, xk)[0]
其中 f 是损失函数,xk 是变量。这是一个 MWE,假设所有 J 都是 1
import numpy as np
import tensorflow as tf
#first I define the variable
n=10 #size of x
x1 = tf.Variable(tf.zeros([n], dtype='float64'))
x2 = tf.placeholder(tf.float64, shape=[n])
#here I define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x2, [n,1])),
tf.reshape(x2, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
#run on test array
xtest = np.ones(n)
res = session.run([f, tf.gradients(f, x1)[0]],
feed_dict={x1 : xtest,
x2 : xtest})
assert res[0] == 1000
assert all(res[1] == np.array([100 for _ in xrange(n)]))
我需要独立调用 run 多次,我想将变量赋值的数量减少到只有一个,因为 x1、x2 指的是同一个向量。
n=200(在 GeForce GTX 650 上)相关示例的一些分析表明
- cuMemcpyDtoHAsync 占用 63% 的时间
- cuMemcpyHtoDAsync 18% 和
- cuEventRecord 18%。
(此 mwe 的结果相似)
因此,在 GPU 上执行计算时,分配是最昂贵的操作。显然,随着 n 的增加,开销变得更糟,因此部分抵消了使用 GPU 的好处。
关于如何通过仅传输一次 x 来减少开销的任何建议?
还有关于如何减少任何其他开销的任何其他建议将不胜感激。
编辑
为了展示实际问题,我将遵循 mrry 的建议。 如果我用 x1 替换 x2 的所有实例,那么 MWE 将如下所示
#first I define the variable
n=10 #size of x
x1 = tf.Variable(tf.zeros([n], dtype='float64'))
#here I define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x1, [n,1])),
tf.reshape(x1, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
#run on test array
xtest = np.ones(n)
session.run(x1.assign(xtest))
res = session.run([f, tf.gradients(f, x1)[0]])
assert res[0] == 1000
for g in res[1]:
assert g == 100
并且第二个断言会失败,因为梯度的每个条目都是 300 而不是 100,因为它应该是。原因是虽然 xi、xj、xk 都指代相同的向量,但它们在符号上是不同的:用相同的变量替换所有 x 将导致 x^3 的导数,即 3*x^2,因此结果第二个 MWE。
P.S。为了清楚起见,我还明确分配了 x1
实现您想要的结果的一种方法是使用 tf.stop_gradient() 操作来制作变量 x1 的有效副本,而不会影响梯度:
import numpy as np
import tensorflow as tf
# First define the variable.
n = 10 # size of x
x1 = tf.Variable(tf.zeros([n], dtype=tf.float64))
x2 = tf.stop_gradient(x1)
# Now define the cost function
f_tensor = tf.mul(tf.mul(tf.reshape(x1, [n]),
tf.reshape(x2, [n,1])),
tf.reshape(x2, [n,1,1]))
f = tf.reduce_sum(f_tensor)
session = tf.Session()
init = tf.initialize_all_variables()
session.run(init)
# Run on test array
xtest = np.ones(n)
res = session.run([f, tf.gradients(f, x1)[0]],
feed_dict={x1 : xtest})
assert res[0] == 1000
for g in res[1]:
assert g == 100
我无法在上面评论(信誉不够),但请注意分析梯度应该是
$$ \frac{\partial f}{\partial x_k} = \sum_{ij} J_{ijk} x_i x_j + \sum_{ij} J_{ikj} x_i x_j + \sum_{ij} J_{kij} x_i x_j。 $$