fftw3 for poisson with dirichlet boundary condition for all side of computational domain
fftw3 for poisson with dirichlet boundary condition for all side of computational domain
我正在尝试用 Dirichlet 边界条件为计算域的四个边求解 Poison 方程。众所周知,我应该使用 FFTW_RODFT00 来满足条件。但是,结果不是correct.Could请大家帮帮我?
#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N1=100;
int N2=100;
double pi = 3.141592653589793;
double L1 = 2.0;
double dx = L1/(double)(N1-1);
double L2= 2.0;
double dy=L2/(double)(N2-1);
double invL1s=1.0/(L1*L1);
double invL2s=1.0/(L2*L2);
std::vector<double> in1(N1*N2,0.0);
std::vector<double> in2(N1*N2,0.0);
std::vector<double> out1(N1*N2,0.0);
std::vector<double> out2(N1*N2,0.0);
std::vector<double> X(N1,0.0);
std::vector<double> Y(N2,0.0);
fftw_plan p, q;
int i,j;
p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
int l=-1;
for(i = 0;i <N1;i++){
X[i] =-1.0+(double)i*dx ;
for(j = 0;j<N2;j++){
l=l+1;
Y[j] =-1.0+ (double)j*dy ;
in1[l]= sin(pi*X[i]) + sin(pi*Y[j]) ; // row major ordering
}
}
fftw_execute(p);
l=-1;
for ( i = 0; i < N1; i++){ // f = g / ( kx² + ky² )
for( j = 0; j < N2; j++){
l=l+1;
double fact=0;
in2[l]=0;
if(2*i<N1){
fact=((double)i*i)*invL1s;;
}else{
fact=((double)(N1-i)*(N1-i))*invL1s;
}
if(2*j<N2){
fact+=((double)j*j)*invL2s;
}else{
fact+=((double)(N2-j)*(N2-j))*invL2s;
}
if(fact!=0){
in2[l] = out1[l]/fact;
}else{
in2[l] = 0.0;
}
}
}
fftw_execute(q);
l=-1;
double erl1 = 0.;
for ( i = 0; i < N1; i++) {
for( j = 0; j < N2; j++){
l=l+1;
erl1 +=1.0/pi/pi*fabs( in1[l]- 0.25*out2[l]/((double)(N1-1))/((double)(N2-1)));
printf("%3d %10.5f %10.5f\n", l, in1[l], 0.25*out2[l]/((double)(N1-1))/((double)(N2-1)));
}
}
cout<<"error=" <<erl1 <<endl ;
fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();
return 0;
}
我认出了我在 and the code I provided in my answer to Confusion testing fftw3 - poisson equation 2d test中提供给你的一个技巧,它是根据提问者@Charles_P的代码改编的!请考虑在以后的问题中添加指向这些 url 的链接!
Confusion testing fftw3 - poisson equation 2d test的答案专门针对周期性边界条件的情况。所以这里有一些修改来解决Dirichlet边界条件的情况。
fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00,FFTW_EXHAUSTIVE)对应于I型离散正弦变换as defined by the FFTW library:
%5Cfrac%7Bk+1%7D%7Bn+1%7D%5Cright))
它的意思在https://en.wikipedia.org/wiki/Discrete_sine_transform中有很好的描述。如果 FFTW 数组的大小为 N1=4 且其值为 [a,b,c,d],则包含边界的完整数组为 [0,a,b,c,d,0]。因此空间步长是:
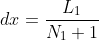
第I类夏令时的频率f_k为:
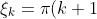%5Cfrac1%7BL_1%7D)
I型DST的倒数就是I型DST,除了比例因子(见http://www.fftw.org/doc/1d-Real_002dodd-DFTs-_0028DSTs_0029.html#g_t1d-Real_002dodd-DFTs-_0028DSTs_0029),这里4.(N1+1).(N2+1).
最后,测试用例必须适应狄利克雷边界条件的情况。实际上,在大小为 L1,L2 的框上,函数 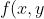=%5Csin(%5Cpi%5Cfrac%7Bx%7D%7BL_1%7D)+%5Csin(%5Cpi%5Cfrac%7By%7D%7BL_2%7D)) 不遵守 Diriclet 边界条件。实际上,即使源项相同,满足周期性边界条件的解也可能与满足 Dirichelt 边界条件的解不同。相反,可以测试两个源术语:
不遵守 Diriclet 边界条件。实际上,即使源项相同,满足周期性边界条件的解也可能与满足 Dirichelt 边界条件的解不同。相反,可以测试两个源术语:
源词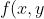=%5Csin(%5Cpi%5Cfrac%7Bx%7D%7BL_1%7D).%5Csin(%5Cpi%5Cfrac%7By%7D%7BL_2%7D)) 对应夏令时的单一频率。
对应夏令时的单一频率。
源项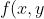=2x(L_1-x)+2y(L_2-y)) 直接推导出解
直接推导出解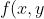=x(L_1-x)y(L_2-y))
最后,这是一个使用 FFTW 库的 I 类 DST 求解 2D 泊松方程的代码:
#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N1=100;
int N2=200;
double pi = 3.141592653589793;
double L1 = 1.0;
double dx = L1/(double)(N1+1);//+ instead of -1
double L2= 5.0;
double dy=L2/(double)(N2+1);
double invL1s=1.0/(L1*L1);
double invL2s=1.0/(L2*L2);
std::vector<double> in1(N1*N2,0.0);
std::vector<double> in2(N1*N2,0.0);
std::vector<double> out1(N1*N2,0.0);
std::vector<double> out2(N1*N2,0.0);
std::vector<double> X(N1,0.0);
std::vector<double> Y(N2,0.0);
fftw_plan p, q;
int i,j;
p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
int l=0;
for(i = 0;i <N1;i++){
for(j = 0;j<N2;j++){
X[i] =dx+(double)i*dx ;
Y[j] =dy+ (double)j*dy ;
//in1[l]= sin(pi*X[i])*sin(pi*Y[j]) ; // row major ordering
in1[l]=2*Y[j]*(L2-Y[j])+2*X[i]*(L1-X[i]);
l=l+1;
}
}
fftw_execute(p);
l=-1;
for ( i = 0; i < N1; i++){ // f = g / ( kx² + ky² )
for( j = 0; j < N2; j++){
l=l+1;
double fact=0;
fact=pi*pi*((double)(i+1)*(i+1))*invL1s;
fact+=pi*pi*((double)(j+1)*(j+1))*invL2s;
in2[l] = out1[l]/fact;
}
}
fftw_execute(q);
l=-1;
double erl1 = 0.;
for ( i = 0; i < N1; i++) {
for( j = 0; j < N2; j++){
l=l+1;
X[i] =dx+(double)i*dx ;
Y[j] =dy+ (double)j*dy ;
//double res=0.5/pi/pi*in1[l];
double res=X[i]*(L1-X[i])*Y[j]*(L2-Y[j]);
erl1 +=pow(fabs(res- 0.25*out2[l]/((double)(N1+1))/((double)(N2+1))),2);
printf("%3d %10.5g %10.5g\n", l, res, 0.25*out2[l]/((double)(N1+1))/((double)(N2+1)));
}
}
erl1=erl1/((double)N1*N2);
cout<<"error=" <<sqrt(erl1) <<endl ;
fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();
return 0;
}
由g++ main.cpp -o main -lfftw3 -Wall.
编译
编辑:如何计算对每个频率的响应?
FFT-based的思想是将解表示为函数的线性组合:
- 在周期性边界条件的情况下,使用FFT。基本函数是:
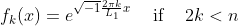
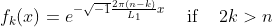
在 Dirichlet 边界条件的情况下,使用 type-I DST。在 x=0 和 x=L1 处为 0 的基函数是:
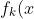=%5Csin%5Cleft(%5Cfrac%7B%5Cpi&space;(k+1)%7D%7BL_1%7Dx%5Cright))
在诺伊曼边界条件的情况下,使用type-I DCT。基本函数是:
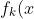=%5Ccos%5Cleft(%5Cfrac%7B%5Cpi&space;k%7D%7BL_1%7Dx%5Cright))
它们的导数在 x=0 和 x=L1 处为空。
让我们计算 type-I DST 的分量 f_k 的二阶导数:
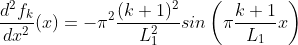
因此,解的 DST 的分量 k 对应于源项的 DST 的分量 k,按因子
缩放
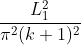
我正在尝试用 Dirichlet 边界条件为计算域的四个边求解 Poison 方程。众所周知,我应该使用 FFTW_RODFT00 来满足条件。但是,结果不是correct.Could请大家帮帮我?
#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N1=100;
int N2=100;
double pi = 3.141592653589793;
double L1 = 2.0;
double dx = L1/(double)(N1-1);
double L2= 2.0;
double dy=L2/(double)(N2-1);
double invL1s=1.0/(L1*L1);
double invL2s=1.0/(L2*L2);
std::vector<double> in1(N1*N2,0.0);
std::vector<double> in2(N1*N2,0.0);
std::vector<double> out1(N1*N2,0.0);
std::vector<double> out2(N1*N2,0.0);
std::vector<double> X(N1,0.0);
std::vector<double> Y(N2,0.0);
fftw_plan p, q;
int i,j;
p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
int l=-1;
for(i = 0;i <N1;i++){
X[i] =-1.0+(double)i*dx ;
for(j = 0;j<N2;j++){
l=l+1;
Y[j] =-1.0+ (double)j*dy ;
in1[l]= sin(pi*X[i]) + sin(pi*Y[j]) ; // row major ordering
}
}
fftw_execute(p);
l=-1;
for ( i = 0; i < N1; i++){ // f = g / ( kx² + ky² )
for( j = 0; j < N2; j++){
l=l+1;
double fact=0;
in2[l]=0;
if(2*i<N1){
fact=((double)i*i)*invL1s;;
}else{
fact=((double)(N1-i)*(N1-i))*invL1s;
}
if(2*j<N2){
fact+=((double)j*j)*invL2s;
}else{
fact+=((double)(N2-j)*(N2-j))*invL2s;
}
if(fact!=0){
in2[l] = out1[l]/fact;
}else{
in2[l] = 0.0;
}
}
}
fftw_execute(q);
l=-1;
double erl1 = 0.;
for ( i = 0; i < N1; i++) {
for( j = 0; j < N2; j++){
l=l+1;
erl1 +=1.0/pi/pi*fabs( in1[l]- 0.25*out2[l]/((double)(N1-1))/((double)(N2-1)));
printf("%3d %10.5f %10.5f\n", l, in1[l], 0.25*out2[l]/((double)(N1-1))/((double)(N2-1)));
}
}
cout<<"error=" <<erl1 <<endl ;
fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();
return 0;
}
我认出了我在
Confusion testing fftw3 - poisson equation 2d test的答案专门针对周期性边界条件的情况。所以这里有一些修改来解决Dirichlet边界条件的情况。
fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00,FFTW_EXHAUSTIVE)对应于I型离散正弦变换as defined by the FFTW library:
它的意思在https://en.wikipedia.org/wiki/Discrete_sine_transform中有很好的描述。如果 FFTW 数组的大小为 N1=4 且其值为 [a,b,c,d],则包含边界的完整数组为 [0,a,b,c,d,0]。因此空间步长是:
第I类夏令时的频率f_k为:
I型DST的倒数就是I型DST,除了比例因子(见http://www.fftw.org/doc/1d-Real_002dodd-DFTs-_0028DSTs_0029.html#g_t1d-Real_002dodd-DFTs-_0028DSTs_0029),这里4.(N1+1).(N2+1).
最后,测试用例必须适应狄利克雷边界条件的情况。实际上,在大小为 L1,L2 的框上,函数 不遵守 Diriclet 边界条件。实际上,即使源项相同,满足周期性边界条件的解也可能与满足 Dirichelt 边界条件的解不同。相反,可以测试两个源术语:
源词
对应夏令时的单一频率。
源项
直接推导出解
最后,这是一个使用 FFTW 库的 I 类 DST 求解 2D 泊松方程的代码:
#include <stdio.h>
#include <math.h>
#include <cmath>
#include <fftw3.h>
#include <iostream>
#include <vector>
using namespace std;
int main() {
int N1=100;
int N2=200;
double pi = 3.141592653589793;
double L1 = 1.0;
double dx = L1/(double)(N1+1);//+ instead of -1
double L2= 5.0;
double dy=L2/(double)(N2+1);
double invL1s=1.0/(L1*L1);
double invL2s=1.0/(L2*L2);
std::vector<double> in1(N1*N2,0.0);
std::vector<double> in2(N1*N2,0.0);
std::vector<double> out1(N1*N2,0.0);
std::vector<double> out2(N1*N2,0.0);
std::vector<double> X(N1,0.0);
std::vector<double> Y(N2,0.0);
fftw_plan p, q;
int i,j;
p = fftw_plan_r2r_2d(N1,N2, in1.data(), out1.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
q = fftw_plan_r2r_2d(N1,N2, in2.data(), out2.data(), FFTW_RODFT00, FFTW_RODFT00, FFTW_EXHAUSTIVE);
int l=0;
for(i = 0;i <N1;i++){
for(j = 0;j<N2;j++){
X[i] =dx+(double)i*dx ;
Y[j] =dy+ (double)j*dy ;
//in1[l]= sin(pi*X[i])*sin(pi*Y[j]) ; // row major ordering
in1[l]=2*Y[j]*(L2-Y[j])+2*X[i]*(L1-X[i]);
l=l+1;
}
}
fftw_execute(p);
l=-1;
for ( i = 0; i < N1; i++){ // f = g / ( kx² + ky² )
for( j = 0; j < N2; j++){
l=l+1;
double fact=0;
fact=pi*pi*((double)(i+1)*(i+1))*invL1s;
fact+=pi*pi*((double)(j+1)*(j+1))*invL2s;
in2[l] = out1[l]/fact;
}
}
fftw_execute(q);
l=-1;
double erl1 = 0.;
for ( i = 0; i < N1; i++) {
for( j = 0; j < N2; j++){
l=l+1;
X[i] =dx+(double)i*dx ;
Y[j] =dy+ (double)j*dy ;
//double res=0.5/pi/pi*in1[l];
double res=X[i]*(L1-X[i])*Y[j]*(L2-Y[j]);
erl1 +=pow(fabs(res- 0.25*out2[l]/((double)(N1+1))/((double)(N2+1))),2);
printf("%3d %10.5g %10.5g\n", l, res, 0.25*out2[l]/((double)(N1+1))/((double)(N2+1)));
}
}
erl1=erl1/((double)N1*N2);
cout<<"error=" <<sqrt(erl1) <<endl ;
fftw_destroy_plan(p); fftw_destroy_plan(q); fftw_cleanup();
return 0;
}
由g++ main.cpp -o main -lfftw3 -Wall.
编辑:如何计算对每个频率的响应?
FFT-based的思想是将解表示为函数的线性组合:
- 在周期性边界条件的情况下,使用FFT。基本函数是:
在 Dirichlet 边界条件的情况下,使用 type-I DST。在
x=0和x=L1处为 0 的基函数是:在诺伊曼边界条件的情况下,使用type-I DCT。基本函数是:
它们的导数在 x=0 和 x=L1 处为空。
让我们计算 type-I DST 的分量 f_k 的二阶导数:
因此,解的 DST 的分量 k 对应于源项的 DST 的分量 k,按因子