最简单公式中的多通道盲解卷积：如何解决？
Multichannel blind deconvolution in the simplest formulation: how to solve?
最近开始研究反卷积算法，遇到了如下采集模型：
%20=%20(f%5Cast%20h)(x,y)%20+%20n(x,y))
其中f是原始（潜在）图像，g是输入（观测）图像，h 是点扩散函数（退化核），n是随机加性噪声，*是卷积算子。
如果我们知道 g 和 h，那么我们可以使用 Richardson-Lucy 算法恢复 f：
%20,%20%5Cend%7Bmatrix%7D)
其中%20=%20h(W-x%20-%201,H-y%20-%201))
,(W,H)是h的矩形支撑的大小，乘法和除法是逐点地。用 C++ 编写代码足够简单，所以我就这样做了。事实证明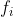 
近似于 f 而 i 小于一些 m 和然后它开始迅速衰减。所以算法只需要停在这个 m - 最令人满意的迭代。
如果点扩散函数g也不知道那么这个问题就是盲目的，可以应用Richardson-Lucy算法的修改：
对于 f 的初始猜测，我们可以像以前一样采用 g，对于 h 我们可以采用普通的 PSF，或任何看起来类似于观察到的图像退化的简单形式。该算法在模拟数据上也能正常工作。
现在考虑多帧盲反卷积问题，采集模型如下：
%20=%20(f%5Cast%20h_1)(x,y)%20+%20n_1(x,y)%5C%5C%20%5Cldots%20%5C%5C%20g_k(x,%20y)%20=%20(f%5Cast%20h_k)(x,y)%20+%20n_k(x,y)%20%5Cend%7Bcases%7D)
有没有办法开发 Richardson-Lucy 算法来解决这个公式中的问题？如果没有，有没有其他的迭代过程来恢复f，不会比前面的复杂很多？
根据您的采集模型，潜像 (f) 保持不变，而观察到的图像因 psf 和噪声模型不同而不同。一种看待它的方法是运动模糊问题，其中清晰且无噪声的图像 (f) 被运动模糊内核破坏。由于这是一个病态问题，在大多数文献中，它是通过估计模糊核和潜像来迭代解决的。你解决这个问题的方式完全取决于你的 objective 功能。
例如，在一些论文中，IRLS 用于估计模糊核。你可以找到很多这方面的文献。
- 如果你想使用 Richardson Lucy Blind 反卷积，那么只在一帧上使用它。
- 一个策略可以在每次迭代中恢复f，为每个g（观察到的图像）的贡献分配不同的权重。您可以在 objective 函数中加入不同的权重，或者根据估计的模糊核计算它们。
Is there a way to develop Richardson-Lucy algorithm for solving the problem in this formulation?
我不是这方面的专家，但我认为这种构建算法的方法不存在，至少不直接。这是我对此的论点。由于噪声的随机性和图像边缘附近卷积的信息丢失，您描述的第一个问题（当 psf 已知时）已经 ill-posed。您列表中的第二个问题——single-channel 盲反卷积——是前一个问题的扩展。在这种情况下又是欠定的，所以ill-posed性扩大了，所以解决这个问题的方法自然是从解决第一个问题的方法发展而来的。现在，当我们考虑多通道盲解卷积公式时，我们向之前的模型添加了一堆额外的信息，因此问题从欠定变为超定。这是另一种 ill-posedness，因此需要不同的解决方法。
is there any other iterative procedure for recovering f, that wouldn't be much more complicated than the previous ones?
我可以推荐一下 Šroubek 和 Milanfar 在 [1] 中介绍的算法。我不确定您认为它是否复杂得多，但它是迄今为止最新和最强大的之一。问题的表述与你写的完全一样。该算法将 K>1 个图像、psf 大小 L 的上限和四个调整参数作为输入：alpha、beta、 伽马，三角洲。例如，要指定 gamma，您需要估计输入图像上噪声的方差并取最大方差 var，然后 伽马 = 1/var。该算法使用交替最小化解决以下优化问题：
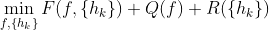
其中 F 是数据保真度项，Q 和 R 是正则项图像和模糊，分别。
算法的详细分析见[1]，不同反卷积公式及其解的集合见[2]。希望能帮助到你。
参考：
菲利普·斯鲁贝克、佩曼·米兰法。 ---- 通过快速交替最小化进行稳健的多通道盲解卷积。
——IEEE 图像处理汇刊，卷。 21号4，2012 年 4 月
Patrizio Campisi，凯伦·埃贾扎里安。 ---- 盲图像反卷积：理论与应用
最近开始研究反卷积算法，遇到了如下采集模型：
其中f是原始（潜在）图像，g是输入（观测）图像，h 是点扩散函数（退化核），n是随机加性噪声，*是卷积算子。 如果我们知道 g 和 h，那么我们可以使用 Richardson-Lucy 算法恢复 f：
其中,(W,H)是h的矩形支撑的大小，乘法和除法是逐点地。用 C++ 编写代码足够简单，所以我就这样做了。事实证明
近似于 f 而 i 小于一些 m 和然后它开始迅速衰减。所以算法只需要停在这个 m - 最令人满意的迭代。
如果点扩散函数g也不知道那么这个问题就是盲目的，可以应用Richardson-Lucy算法的修改：
对于 f 的初始猜测，我们可以像以前一样采用 g，对于 h 我们可以采用普通的 PSF，或任何看起来类似于观察到的图像退化的简单形式。该算法在模拟数据上也能正常工作。
现在考虑多帧盲反卷积问题，采集模型如下：
有没有办法开发 Richardson-Lucy 算法来解决这个公式中的问题？如果没有，有没有其他的迭代过程来恢复f，不会比前面的复杂很多？
根据您的采集模型，潜像 (f) 保持不变，而观察到的图像因 psf 和噪声模型不同而不同。一种看待它的方法是运动模糊问题，其中清晰且无噪声的图像 (f) 被运动模糊内核破坏。由于这是一个病态问题，在大多数文献中，它是通过估计模糊核和潜像来迭代解决的。你解决这个问题的方式完全取决于你的 objective 功能。 例如，在一些论文中，IRLS 用于估计模糊核。你可以找到很多这方面的文献。
- 如果你想使用 Richardson Lucy Blind 反卷积，那么只在一帧上使用它。
- 一个策略可以在每次迭代中恢复f，为每个g（观察到的图像）的贡献分配不同的权重。您可以在 objective 函数中加入不同的权重，或者根据估计的模糊核计算它们。
Is there a way to develop Richardson-Lucy algorithm for solving the problem in this formulation?
我不是这方面的专家，但我认为这种构建算法的方法不存在，至少不直接。这是我对此的论点。由于噪声的随机性和图像边缘附近卷积的信息丢失，您描述的第一个问题（当 psf 已知时）已经 ill-posed。您列表中的第二个问题——single-channel 盲反卷积——是前一个问题的扩展。在这种情况下又是欠定的，所以ill-posed性扩大了，所以解决这个问题的方法自然是从解决第一个问题的方法发展而来的。现在，当我们考虑多通道盲解卷积公式时，我们向之前的模型添加了一堆额外的信息，因此问题从欠定变为超定。这是另一种 ill-posedness，因此需要不同的解决方法。
is there any other iterative procedure for recovering f, that wouldn't be much more complicated than the previous ones?
我可以推荐一下 Šroubek 和 Milanfar 在 [1] 中介绍的算法。我不确定您认为它是否复杂得多，但它是迄今为止最新和最强大的之一。问题的表述与你写的完全一样。该算法将 K>1 个图像、psf 大小 L 的上限和四个调整参数作为输入：alpha、beta、 伽马，三角洲。例如，要指定 gamma，您需要估计输入图像上噪声的方差并取最大方差 var，然后 伽马 = 1/var。该算法使用交替最小化解决以下优化问题：
其中 F 是数据保真度项，Q 和 R 是正则项图像和模糊，分别。
算法的详细分析见[1]，不同反卷积公式及其解的集合见[2]。希望能帮助到你。
参考：
菲利普·斯鲁贝克、佩曼·米兰法。 ---- 通过快速交替最小化进行稳健的多通道盲解卷积。 ——IEEE 图像处理汇刊，卷。 21号4，2012 年 4 月
Patrizio Campisi，凯伦·埃贾扎里安。 ---- 盲图像反卷积：理论与应用