目的是在内存操作的 MMIX 程序集中将最低有效位设置为 0？
Purpose to set to 0 least significant bits in MMIX assembly with memory operations?
在 MMIX 机器的文档中 mmix-doc 第 3 页第 4 段：
We use the notation 
to stand for a number consisting of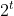 
consecutive bytes starting at location  "k \wedge (2^{64} - 2^{t})")
. (The notation
means that the least significant t bits of k are set to
0, and only the least 64 bits of the resulting address are retained.
...
符号M2t[k]只是一种形式化的符号表达可被 2t.
整除的地址
这个刚定义完就确认了
All accesses to 2t-byte quantities by MMIX are aligned, in the
sense that the first byte is a multiple of 2t.
大多数架构，特别是 RISC 架构，要求内存访问 对齐，这意味着地址必须是所访问大小的倍数。
因此，例如，从内存中读取一个 64 位字（MMIX 表示法中的八进制）需要地址可以被 8 整除，因为 MMIX 内存是字节可寻址的 (1) 并且有 8八进制中的字节。
如果所有可能的数据大小都是 2 的幂，我们会看到一个模式出现：
Multiples of Multiples of Multiples of
2 4 8
0000 0000 0000
0010 0100 1000
0100 1000
0110 1100
1000
1010
1100
1110
2 的倍数 = 21 的最小位总是设置为零(2)，4 的倍数 = 22 将最小的两个位设置为零，8 = 23 的倍数将最小的三个位设置为零，依此类推。
通常 2t 的倍数将最少的 t 位设置为零。
您可以通过对 t 的归纳来正式证明这一点。
对齐 64 位数字（MMIX 地址的大小 space）的一种方法是清除其较低的 t 位，这可以通过执行AND 操作，掩码形式为
11111...1000...0
\ / \ /
64 - t t
这样的mask可以表示为264 - 2t。
例如，264 是一个很大的数字，假设地址 space 只有 25.
假设我们有二进制地址 17h 或 10111b，假设我们想将其与八进制对齐。
Octas 是 8 个字节，23 所以我们需要清除低 3 位并保留其他 2 位。
要使用的掩码是 11000b 或十六进制的 18h。这个数字是 25-23 = 32 - 8 = 24 = 18h.
如果我们在 17h 和 18h 之间执行布尔与，我们得到 10h，这是对齐的地址。
这解释了符号 k ∧ (264 − 2t) 紧跟其后，"wedge"符号∧是逻辑与。
所以这个符号只是 "pictures" 对齐地址所需的步骤 k.
注意记号 k ∨ (2t − 1) 也被引入，这是互补，∨ 是或，整个效果是有较低的 t 位设置为 1.
这是大小为 2t.
的对齐访问占用的最大地址
符号本身用于解释 endianess.
如果您想知道为什么对齐访问很重要，这与硬件实现有关。
长话短说，CPU 内存接口具有预定义的大小，尽管内存是字节可寻址的，比如 64 位。
因此 CPU 以 64 位块的形式访问内存，每个块都从 64 位的地址倍数开始（即 aligned 在 8 字节上）。
访问未对齐的位置可能需要 CPU 执行两次访问：
CPU reading an octa at address 2, we need bytes at 2, 3, 4 and 5.
Address 0 1 2 3 4 5 6 7 8 9 A B ...
\ / \ /
A B
CPU read octa at 0 (access A) and octa at 4 (access B), then combines the two reads.
RISC 机器倾向于避免这种复杂性并完全禁止未对齐的访问。
(1) 引用：“如果 k 是任何无符号八字节，M[k] 是一个 1 字节
数量”。
(2) 20 = 1 是 2 的唯一奇次方，所以你可以猜到通过删除它我们只得到偶数。
在 MMIX 机器的文档中 mmix-doc 第 3 页第 4 段：
We use the notation
符号M2t[k]只是一种形式化的符号表达可被 2t.
整除的地址这个刚定义完就确认了
All accesses to 2t-byte quantities by MMIX are aligned, in the sense that the first byte is a multiple of 2t.
大多数架构，特别是 RISC 架构，要求内存访问 对齐，这意味着地址必须是所访问大小的倍数。
因此，例如，从内存中读取一个 64 位字（MMIX 表示法中的八进制）需要地址可以被 8 整除，因为 MMIX 内存是字节可寻址的 (1) 并且有 8八进制中的字节。
如果所有可能的数据大小都是 2 的幂，我们会看到一个模式出现：
Multiples of Multiples of Multiples of
2 4 8
0000 0000 0000
0010 0100 1000
0100 1000
0110 1100
1000
1010
1100
1110
2 的倍数 = 21 的最小位总是设置为零(2)，4 的倍数 = 22 将最小的两个位设置为零，8 = 23 的倍数将最小的三个位设置为零，依此类推。
通常 2t 的倍数将最少的 t 位设置为零。
您可以通过对 t 的归纳来正式证明这一点。
对齐 64 位数字（MMIX 地址的大小 space）的一种方法是清除其较低的 t 位，这可以通过执行AND 操作，掩码形式为
11111...1000...0
\ / \ /
64 - t t
这样的mask可以表示为264 - 2t。
例如，264 是一个很大的数字，假设地址 space 只有 25.
假设我们有二进制地址 17h 或 10111b，假设我们想将其与八进制对齐。
Octas 是 8 个字节，23 所以我们需要清除低 3 位并保留其他 2 位。
要使用的掩码是 11000b 或十六进制的 18h。这个数字是 25-23 = 32 - 8 = 24 = 18h.
如果我们在 17h 和 18h 之间执行布尔与，我们得到 10h，这是对齐的地址。
这解释了符号 k ∧ (264 − 2t) 紧跟其后，"wedge"符号∧是逻辑与。
所以这个符号只是 "pictures" 对齐地址所需的步骤 k.
注意记号 k ∨ (2t − 1) 也被引入，这是互补，∨ 是或，整个效果是有较低的 t 位设置为 1.
这是大小为 2t.
的对齐访问占用的最大地址
符号本身用于解释 endianess.
如果您想知道为什么对齐访问很重要，这与硬件实现有关。
长话短说，CPU 内存接口具有预定义的大小，尽管内存是字节可寻址的，比如 64 位。
因此 CPU 以 64 位块的形式访问内存，每个块都从 64 位的地址倍数开始（即 aligned 在 8 字节上）。
访问未对齐的位置可能需要 CPU 执行两次访问：
CPU reading an octa at address 2, we need bytes at 2, 3, 4 and 5.
Address 0 1 2 3 4 5 6 7 8 9 A B ...
\ / \ /
A B
CPU read octa at 0 (access A) and octa at 4 (access B), then combines the two reads.
RISC 机器倾向于避免这种复杂性并完全禁止未对齐的访问。
(1) 引用：“如果 k 是任何无符号八字节，M[k] 是一个 1 字节 数量”。
(2) 20 = 1 是 2 的唯一奇次方，所以你可以猜到通过删除它我们只得到偶数。