Pyomo 在具有时间序列缺失值的 ODE 系统中的参数估计
Pyomo's parameter estimation in an ODE system with missing values in time series
我有一个包含 7 个方程的 ODE 系统，用于解释一组特定的微生物动力学形式：
其中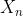 
是所涉及的不同化学和微生物物种（甚至是化合物的子索引），
是产率系数，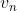
是伪-反应：
我正在使用 Pyomo 来估计我所有的未知参数，这些参数基本上都是屈服系数和动力学常数（总共 15 个）。
以下代码在与每个动态变量的完整实验时间序列一起使用时完美运行：
from pyomo.environ import *
from pyomo.dae import *
m = AbstractModel()
m.t = ContinuousSet()
m.MEAS_t = Set(within=m.t) # Measurement times, must be subset of t
m.x1_meas = Param(m.MEAS_t)
m.x2_meas = Param(m.MEAS_t)
m.x3_meas = Param(m.MEAS_t)
m.x4_meas = Param(m.MEAS_t)
m.x5_meas = Param(m.MEAS_t)
m.x6_meas = Param(m.MEAS_t)
m.x7_meas = Param(m.MEAS_t)
m.x1 = Var(m.t,within=PositiveReals)
m.x2 = Var(m.t,within=PositiveReals)
m.x3 = Var(m.t,within=PositiveReals)
m.x4 = Var(m.t,within=PositiveReals)
m.x5 = Var(m.t,within=PositiveReals)
m.x6 = Var(m.t,within=PositiveReals)
m.x7 = Var(m.t,within=PositiveReals)
m.k1 = Var(within=PositiveReals)
m.k2 = Var(within=PositiveReals)
m.k3 = Var(within=PositiveReals)
m.k4 = Var(within=PositiveReals)
m.k5 = Var(within=PositiveReals)
m.k6 = Var(within=PositiveReals)
m.k7 = Var(within=PositiveReals)
m.k8 = Var(within=PositiveReals)
m.k9 = Var(within=PositiveReals)
m.y1 = Var(within=PositiveReals)
m.y2 = Var(within=PositiveReals)
m.y3 = Var(within=PositiveReals)
m.y4 = Var(within=PositiveReals)
m.y5 = Var(within=PositiveReals)
m.y6 = Var(within=PositiveReals)
m.x1dot = DerivativeVar(m.x1,wrt=m.t)
m.x2dot = DerivativeVar(m.x2,wrt=m.t)
m.x3dot = DerivativeVar(m.x3,wrt=m.t)
m.x4dot = DerivativeVar(m.x4,wrt=m.t)
m.x5dot = DerivativeVar(m.x5,wrt=m.t)
m.x6dot = DerivativeVar(m.x6,wrt=m.t)
m.x7dot = DerivativeVar(m.x7,wrt=m.t)
def _init_conditions(m):
yield m.x1[0] == 51.963
yield m.x2[0] == 6.289
yield m.x3[0] == 0
yield m.x4[0] == 6.799
yield m.x5[0] == 0
yield m.x6[0] == 4.08
yield m.x7[0] == 0
m.init_conditions=ConstraintList(rule=_init_conditions)
def _x1dot(m,i):
if i==0:
return Constraint.Skip
return m.x1dot[i] == - m.y1*m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.y2*m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i])
m.x1dotcon = Constraint(m.t, rule=_x1dot)
def _x2dot(m,i):
if i==0:
return Constraint.Skip
return m.x2dot[i] == m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.k7*m.x2[i]*m.x3[i]
m.x2dotcon = Constraint(m.t, rule=_x2dot)
def _x3dot(m,i):
if i==0:
return Constraint.Skip
return m.x3dot[i] == m.y3*m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.y4*m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i])
m.x3dotcon = Constraint(m.t, rule=_x3dot)
def _x4dot(m,i):
if i==0:
return Constraint.Skip
return m.x4dot[i] == m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i]) - m.k8*m.x4[i]*m.x3[i]
m.x4dotcon = Constraint(m.t, rule=_x4dot)
def _x5dot(m,i):
if i==0:
return Constraint.Skip
return m.x5dot[i] == m.y5*m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i])
m.x5dotcon = Constraint(m.t, rule=_x5dot)
def _x6dot(m,i):
if i==0:
return Constraint.Skip
return m.x6dot[i] == m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i]) - m.k9*m.x6[i]*m.x7[i]
m.x6dotcon = Constraint(m.t, rule=_x6dot)
def _x7dot(m,i):
if i==0:
return Constraint.Skip
return m.x7dot[i] == m.y6*m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i])
m.x7dotcon = Constraint(m.t, rule=_x7dot)
def _obj(m):
return sum((m.x1[i]-m.x1_meas[i])**2+(m.x2[i]-m.x2_meas[i])**2+(m.x3[i]-m.x3_meas[i])**2+(m.x4[i]-m.x4_meas[i])**2+(m.x5[i]-m.x5_meas[i])**2+(m.x6[i]-m.x6_meas[i])**2+(m.x7[i]-m.x7_meas[i])**2 for i in m.MEAS_t)
m.obj = Objective(rule=_obj)
m.pprint()
instance = m.create_instance('exp.dat')
instance.t.pprint()
discretizer = TransformationFactory('dae.collocation')
discretizer.apply_to(instance,nfe=30)#,ncp=3)
solver=SolverFactory('ipopt')
results = solver.solve(instance,tee=True)
但是，我正在尝试 运行 在另一个实验数据中使用相同的估计程序，这些数据在某些动态变量的一个或最多两个时间序列的末尾具有缺失值。
换句话说，这些完整的实验数据看起来像（在.dat文件中）：
set t := 0 6 12 18 24 30 36 42 48 54 60 66 72 84 96 120 144;
set MEAS_t := 0 6 12 18 24 30 36 42 48 54 60 66 72 84 96 120 144;
param x1_meas :=
0 51.963
6 43.884
12 24.25
18 26.098
24 11.871
30 4.607
36 1.714
42 4.821
48 5.409
54 3.701
60 3.696
66 1.544
72 4.428
84 1.086
96 2.337
120 2.837
144 3.486
;
param x2_meas :=
0 6.289
6 6.242
12 7.804
18 7.202
24 6.48
30 5.833
36 6.644
42 5.741
48 4.568
54 4.252
60 5.603
66 5.167
72 4.399
84 4.773
96 4.801
120 3.866
144 3.847
;
param x3_meas :=
0 0
6 2.97
12 9.081
18 9.62
24 6.067
30 11.211
36 16.213
42 10.215
48 20.106
54 22.492
60 5.637
66 5.636
72 13.85
84 4.782
96 9.3
120 4.267
144 7.448
;
param x4_meas :=
0 6.799
6 7.73
12 7.804
18 8.299
24 8.208
30 8.523
36 8.507
42 8.656
48 8.49
54 8.474
60 8.203
66 8.127
72 8.111
84 8.064
96 6.845
120 6.721
144 6.162
;
param x5_meas :=
0 0
6 0.267
12 0.801
18 1.256
24 1.745
30 5.944
36 3.246
42 7.787
48 7.991
54 6.943
60 8.593
66 8.296
72 6.85
84 8.021
96 7.667
120 7.209
144 8.117
;
param x6_meas :=
0 4.08
6 4.545
12 4.784
18 4.888
24 5.293
30 5.577
36 5.802
42 5.967
48 6.386
54 6.115
60 6.625
66 6.835
72 6.383
84 6.605
96 5.928
120 5.354
144 4.975
;
param x7_meas :=
0 0
6 0.152
12 1.616
18 0.979
24 4.033
30 5.121
36 2.759
42 3.541
48 4.278
54 4.141
60 6.139
66 3.219
72 5.319
84 4.328
96 3.621
120 4.208
144 5.93
;
虽然我的一个不完整的数据集可能所有时间序列都是完整的，但像这样：
param x6_meas :=
0 4.08
6 4.545
12 4.784
18 4.888
24 5.293
30 5.577
36 5.802
42 5.967
48 6.386
54 6.115
60 6.625
66 6.835
72 6.383
84 6.605
96 5.928
120 5.354
144 .
;
我知道可以指定 Pyomo 对不同的时间序列取某些变量的导数。然而试了之后还是不行，我猜是因为这些是耦合的ODE。所以基本上我的问题是是否有办法在 Pyomo 中解决这个问题。
提前致谢。
我认为您需要做的就是像这样稍微修改您的 objective 函数：
def _obj(m):
sum1 = sum((m.x1[i]-m.x1_meas[i])**2 for i in m.MEAS_t if i in m.x1_meas.keys())
sum2 = sum((m.x2[i]-m.x2_meas[i])**2 for i in m.MEAS_t if i in m.x2_meas.keys())
sum3 = sum((m.x3[i]-m.x3_meas[i])**2 for i in m.MEAS_t if i in m.x3_meas.keys())
sum4 = sum((m.x4[i]-m.x4_meas[i])**2 for i in m.MEAS_t if i in m.x4_meas.keys())
sum5 = sum((m.x5[i]-m.x5_meas[i])**2 for i in m.MEAS_t if i in m.x5_meas.keys())
sum6 = sum((m.x6[i]-m.x6_meas[i])**2 for i in m.MEAS_t if i in m.x6_meas.keys())
sum7 = sum((m.x7[i]-m.x7_meas[i])**2 for i in m.MEAS_t if i in m.x7_meas.keys())
return sum1+sum2+sum3+sum4+sum5+sum6+sum7
m.obj = Objective(rule=_obj)
这会双重检查 i 是每组测量值的有效索引，然后再将该索引添加到总和中。如果您先验地知道哪些测量集缺少数据，那么您可以通过仅对这些集进行检查并像以前一样对其他集进行求和来简化此功能。
我有一个包含 7 个方程的 ODE 系统，用于解释一组特定的微生物动力学形式：
其中 是所涉及的不同化学和微生物物种（甚至是化合物的子索引），
是产率系数，
是伪-反应：
我正在使用 Pyomo 来估计我所有的未知参数，这些参数基本上都是屈服系数和动力学常数（总共 15 个）。
以下代码在与每个动态变量的完整实验时间序列一起使用时完美运行：
from pyomo.environ import *
from pyomo.dae import *
m = AbstractModel()
m.t = ContinuousSet()
m.MEAS_t = Set(within=m.t) # Measurement times, must be subset of t
m.x1_meas = Param(m.MEAS_t)
m.x2_meas = Param(m.MEAS_t)
m.x3_meas = Param(m.MEAS_t)
m.x4_meas = Param(m.MEAS_t)
m.x5_meas = Param(m.MEAS_t)
m.x6_meas = Param(m.MEAS_t)
m.x7_meas = Param(m.MEAS_t)
m.x1 = Var(m.t,within=PositiveReals)
m.x2 = Var(m.t,within=PositiveReals)
m.x3 = Var(m.t,within=PositiveReals)
m.x4 = Var(m.t,within=PositiveReals)
m.x5 = Var(m.t,within=PositiveReals)
m.x6 = Var(m.t,within=PositiveReals)
m.x7 = Var(m.t,within=PositiveReals)
m.k1 = Var(within=PositiveReals)
m.k2 = Var(within=PositiveReals)
m.k3 = Var(within=PositiveReals)
m.k4 = Var(within=PositiveReals)
m.k5 = Var(within=PositiveReals)
m.k6 = Var(within=PositiveReals)
m.k7 = Var(within=PositiveReals)
m.k8 = Var(within=PositiveReals)
m.k9 = Var(within=PositiveReals)
m.y1 = Var(within=PositiveReals)
m.y2 = Var(within=PositiveReals)
m.y3 = Var(within=PositiveReals)
m.y4 = Var(within=PositiveReals)
m.y5 = Var(within=PositiveReals)
m.y6 = Var(within=PositiveReals)
m.x1dot = DerivativeVar(m.x1,wrt=m.t)
m.x2dot = DerivativeVar(m.x2,wrt=m.t)
m.x3dot = DerivativeVar(m.x3,wrt=m.t)
m.x4dot = DerivativeVar(m.x4,wrt=m.t)
m.x5dot = DerivativeVar(m.x5,wrt=m.t)
m.x6dot = DerivativeVar(m.x6,wrt=m.t)
m.x7dot = DerivativeVar(m.x7,wrt=m.t)
def _init_conditions(m):
yield m.x1[0] == 51.963
yield m.x2[0] == 6.289
yield m.x3[0] == 0
yield m.x4[0] == 6.799
yield m.x5[0] == 0
yield m.x6[0] == 4.08
yield m.x7[0] == 0
m.init_conditions=ConstraintList(rule=_init_conditions)
def _x1dot(m,i):
if i==0:
return Constraint.Skip
return m.x1dot[i] == - m.y1*m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.y2*m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i])
m.x1dotcon = Constraint(m.t, rule=_x1dot)
def _x2dot(m,i):
if i==0:
return Constraint.Skip
return m.x2dot[i] == m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.k7*m.x2[i]*m.x3[i]
m.x2dotcon = Constraint(m.t, rule=_x2dot)
def _x3dot(m,i):
if i==0:
return Constraint.Skip
return m.x3dot[i] == m.y3*m.k1*m.x1[i]*m.x2[i]/(m.k2+m.x1[i]) - m.y4*m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i])
m.x3dotcon = Constraint(m.t, rule=_x3dot)
def _x4dot(m,i):
if i==0:
return Constraint.Skip
return m.x4dot[i] == m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i]) - m.k8*m.x4[i]*m.x3[i]
m.x4dotcon = Constraint(m.t, rule=_x4dot)
def _x5dot(m,i):
if i==0:
return Constraint.Skip
return m.x5dot[i] == m.y5*m.k3*m.x1[i]*m.x4[i]/(m.k4+m.x1[i])
m.x5dotcon = Constraint(m.t, rule=_x5dot)
def _x6dot(m,i):
if i==0:
return Constraint.Skip
return m.x6dot[i] == m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i]) - m.k9*m.x6[i]*m.x7[i]
m.x6dotcon = Constraint(m.t, rule=_x6dot)
def _x7dot(m,i):
if i==0:
return Constraint.Skip
return m.x7dot[i] == m.y6*m.k5*m.x3[i]*m.x6[i]/(m.k6+m.x3[i])
m.x7dotcon = Constraint(m.t, rule=_x7dot)
def _obj(m):
return sum((m.x1[i]-m.x1_meas[i])**2+(m.x2[i]-m.x2_meas[i])**2+(m.x3[i]-m.x3_meas[i])**2+(m.x4[i]-m.x4_meas[i])**2+(m.x5[i]-m.x5_meas[i])**2+(m.x6[i]-m.x6_meas[i])**2+(m.x7[i]-m.x7_meas[i])**2 for i in m.MEAS_t)
m.obj = Objective(rule=_obj)
m.pprint()
instance = m.create_instance('exp.dat')
instance.t.pprint()
discretizer = TransformationFactory('dae.collocation')
discretizer.apply_to(instance,nfe=30)#,ncp=3)
solver=SolverFactory('ipopt')
results = solver.solve(instance,tee=True)
但是，我正在尝试 运行 在另一个实验数据中使用相同的估计程序，这些数据在某些动态变量的一个或最多两个时间序列的末尾具有缺失值。
换句话说，这些完整的实验数据看起来像（在.dat文件中）：
set t := 0 6 12 18 24 30 36 42 48 54 60 66 72 84 96 120 144;
set MEAS_t := 0 6 12 18 24 30 36 42 48 54 60 66 72 84 96 120 144;
param x1_meas :=
0 51.963
6 43.884
12 24.25
18 26.098
24 11.871
30 4.607
36 1.714
42 4.821
48 5.409
54 3.701
60 3.696
66 1.544
72 4.428
84 1.086
96 2.337
120 2.837
144 3.486
;
param x2_meas :=
0 6.289
6 6.242
12 7.804
18 7.202
24 6.48
30 5.833
36 6.644
42 5.741
48 4.568
54 4.252
60 5.603
66 5.167
72 4.399
84 4.773
96 4.801
120 3.866
144 3.847
;
param x3_meas :=
0 0
6 2.97
12 9.081
18 9.62
24 6.067
30 11.211
36 16.213
42 10.215
48 20.106
54 22.492
60 5.637
66 5.636
72 13.85
84 4.782
96 9.3
120 4.267
144 7.448
;
param x4_meas :=
0 6.799
6 7.73
12 7.804
18 8.299
24 8.208
30 8.523
36 8.507
42 8.656
48 8.49
54 8.474
60 8.203
66 8.127
72 8.111
84 8.064
96 6.845
120 6.721
144 6.162
;
param x5_meas :=
0 0
6 0.267
12 0.801
18 1.256
24 1.745
30 5.944
36 3.246
42 7.787
48 7.991
54 6.943
60 8.593
66 8.296
72 6.85
84 8.021
96 7.667
120 7.209
144 8.117
;
param x6_meas :=
0 4.08
6 4.545
12 4.784
18 4.888
24 5.293
30 5.577
36 5.802
42 5.967
48 6.386
54 6.115
60 6.625
66 6.835
72 6.383
84 6.605
96 5.928
120 5.354
144 4.975
;
param x7_meas :=
0 0
6 0.152
12 1.616
18 0.979
24 4.033
30 5.121
36 2.759
42 3.541
48 4.278
54 4.141
60 6.139
66 3.219
72 5.319
84 4.328
96 3.621
120 4.208
144 5.93
;
虽然我的一个不完整的数据集可能所有时间序列都是完整的，但像这样：
param x6_meas :=
0 4.08
6 4.545
12 4.784
18 4.888
24 5.293
30 5.577
36 5.802
42 5.967
48 6.386
54 6.115
60 6.625
66 6.835
72 6.383
84 6.605
96 5.928
120 5.354
144 .
;
我知道可以指定 Pyomo 对不同的时间序列取某些变量的导数。然而试了之后还是不行，我猜是因为这些是耦合的ODE。所以基本上我的问题是是否有办法在 Pyomo 中解决这个问题。
提前致谢。
我认为您需要做的就是像这样稍微修改您的 objective 函数：
def _obj(m):
sum1 = sum((m.x1[i]-m.x1_meas[i])**2 for i in m.MEAS_t if i in m.x1_meas.keys())
sum2 = sum((m.x2[i]-m.x2_meas[i])**2 for i in m.MEAS_t if i in m.x2_meas.keys())
sum3 = sum((m.x3[i]-m.x3_meas[i])**2 for i in m.MEAS_t if i in m.x3_meas.keys())
sum4 = sum((m.x4[i]-m.x4_meas[i])**2 for i in m.MEAS_t if i in m.x4_meas.keys())
sum5 = sum((m.x5[i]-m.x5_meas[i])**2 for i in m.MEAS_t if i in m.x5_meas.keys())
sum6 = sum((m.x6[i]-m.x6_meas[i])**2 for i in m.MEAS_t if i in m.x6_meas.keys())
sum7 = sum((m.x7[i]-m.x7_meas[i])**2 for i in m.MEAS_t if i in m.x7_meas.keys())
return sum1+sum2+sum3+sum4+sum5+sum6+sum7
m.obj = Objective(rule=_obj)
这会双重检查 i 是每组测量值的有效索引，然后再将该索引添加到总和中。如果您先验地知道哪些测量集缺少数据，那么您可以通过仅对这些集进行检查并像以前一样对其他集进行求和来简化此功能。