MATLAB 在不变流形上求解 ODE

Question

我的系统看起来像

dn/dt=f(n,v)
dh/dt=g(h,v)

我想在流形 F(v,n,h)=0 上求解这个方程，v 中的一个非线性函数。我尝试使用 v=fzero(@(x) F(x,n,h),0) 之类的东西来求解每个时间步流形上 v 的值。但这非常慢，而且 ode15s（我的系统是张弛振荡器）无法满足积分公差。如何在 F(v,n,h)=0 定义的流形上找到 ODE 的解？

Answer 1

解决这个问题的一种可能方法是区分 F(v,n,h)=0 等式：

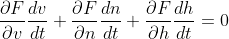
$\frac{\partial F}{\partial v}\frac{dv}{dt}+\frac{\partial F}{\partial n}\frac{dn}{dt}+\frac{\partial F}{\partial h}\frac{dh}{dt}=0$

现在我们可以获得ODE系统

$\frac{dn}{dt}=f(n,v),\, \frac{dh}{dt}=g(h,v),\,\frac{dv}{dt}= -\left.\left( \frac{\partial F}{\partial n}\frac{dn}{dt}+\frac{\partial F}{\partial h}\frac{dh}{dt} \right )\right/ \left( \frac{\partial F}{\partial v} \right )$

或

$\frac{dn}{dt}=f(n,v),\, \frac{dh}{dt}=g(h,v),\,\frac{dv}{dt}= -\left.\left( \frac{\partial F}{\partial n}f(n,v)+\frac{\partial F}{\partial h}g(h,v) \right )\right/ \left( \frac{\partial F}{\partial v} \right )$

按常规方法即可解决

Answer 2

我觉得@LutzL 的评论很有帮助。可以使用 ode15s 设置 DAE 求解器。示例：https://www.mathworks.com/help/matlab/ref/ode15s.html

中的 "Solve Robertson Problem as Semi-Explicit Differential Algebraic Equations (DAEs)" 部分

在我的例子中，我会设置一个矩阵：

M=[zeros(1,3);0,1,0;0,0,1];
options = odeset('Mass',M,'RelTol',1e-5,'AbsTol',1e-6,'MaxStep',0.01);
y0=[v0,n0,h0];
[T,Y]=ode15s(@slow,[0 50],y0,options);

而slow是一个函数定义为：

function dy = slow(t,y)
    v=y(1); n=y(2); h=y(3);
    dy=zeros(3,1);
    dy(1)=F(v,n,h);
    dy(2)=f(n,v);
    dy(3)=g(h,v);
end

MATLAB 在不变流形上求解 ODE

MATLAB solve ODE on invariant manifold

matlab

ode