"pathological" 凸函数的快速优化
Fast optimization of "pathological" convex function
我有一个简单的凸问题,我正在尝试加速解决。我正在求解
的 argmin (theta)
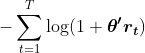
其中 theta 和 rt 是 Nx1.
我可以用 cvxpy 轻松解决这个问题
import numpy as np
from scipy.optimize import minimize
import cvxpy
np.random.seed(123)
T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))
cvtheta = cvxpy.Variable(N)
fn = -sum([cvxpy.log(1 + cvtheta.T * rt) for rt in R])
prob = cvxpy.Problem(cvxpy.Minimize(fn))
prob.solve()
prob.status
#'optimal'
prob.value
# -5.658335088091929
cvtheta.value
# matrix([[-0.82105079],
# [-0.35475695],
# [-0.41984643],
# [ 0.66117397],
# [ 0.46065358]])
但是对于更大的 R 这变得太慢了,所以我正在尝试使用 scipy 的 fmin_cg:
的基于梯度的方法
goalfun 是一个 scipy.minimize 友好的函数,returns 函数值和梯度。
def goalfun(theta, *args):
R = args[0]
N = R.shape[1]
common = (1 + np.sum(theta * R, axis=1))**-1
if np.any( common < 0 ):
return 1e2, 1e2 * np.ones(N)
fun = np.sum(np.log(common))
thetaprime = np.tile(theta, (N, 1)).T
np.fill_diagonal(thetaprime, np.ones(N))
grad = np.sum(np.dot(R, thetaprime) * common[:, None], axis=0)
return fun, grad
确保函数和梯度正确:
goalfun(np.squeeze(np.asarray(cvtheta.value)), R)
# (-5.6583350819293603,
# array([ -9.12423065e-09, -3.36854633e-09, -1.00983679e-08,
# -1.49619901e-08, -1.22987872e-08]))
但是解决这个问题只会产生垃圾,而不管 method、迭代等等。(唯一会产生 Optimization terminated successfully 的是如果 x0 实际上等于最优 θ)
x0 = np.random.rand(R.shape[1])
minimize(fun=goalfun, x0=x0, args=R, jac=True, method='CG')
# fun: 3.3690101669818775
# jac: array([-11.07449021, -14.04017873, -13.38560561, -5.60375334, -2.89210078])
# message: 'Desired error not necessarily achieved due to precision loss.'
# nfev: 25
# nit: 1
# njev: 13
# status: 2
# success: False
# x: array([ 0.00892177, 0.24404118, 0.51627475, 0.21119326, -0.00831957])
即cvxpy 轻松处理的这个看似无害的问题,对于非凸求解器来说完全是病态的。这个问题真的那么讨厌,还是我遗漏了什么?有什么替代方法可以加快速度?
我认为问题在于 theta 可能会使 log 论点变成否定的。看来您已经确定了这个问题,并且在这种情况下 goalfun return 元组 (100,100*ones(N)) 显然是一种启发式尝试,建议求解器认为此 "solution" 是不是 可取的 。但是,必须施加更强的条件,即 "solution" 不 可行 。当然,这可以通过提供适当的约束来完成。 (有趣的是,cvxpy 似乎可以自动处理这个问题。)
这是一个示例 运行,无需提供衍生工具。注意使用可行的初始估计 x0.
np.random.seed(123)
T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))
def goalfun(theta, *args):
R = args[0]
N = R.shape[1]
common = (1 + np.sum(theta * R, axis=1))**-1
return np.sum(np.log(common))
def con_fun(theta, *args):
R = args[0]
return 1+np.sum(theta * R, axis=1)
cons = ({'type': 'ineq', 'fun': lambda x: con_fun(x, R)})
x0 = np.zeros(R.shape[1])
minimize(fun=goalfun, x0=x0, args=R, constraints=cons)
fun: -5.658334806882614
jac: array([ 0.0019, -0.0004, -0.0003, 0.0005, -0.0015, 0. ]) message: 'Optimization terminated successfully.'
nfev: 92
nit: 12
njev: 12 status: 0 success: True
x: array([-0.8209, -0.3547, -0.4198, 0.6612, 0.4605])
请注意,当我 运行 这样做时,我收到 invalid value encountered in log 警告,表明在搜索的某个时刻检查了 theta 的值,该值几乎不满足约束条件。但是,结果与 cvxpy 的结果相当接近。当在 cvxpy.Problem 公式中明确施加约束时,检查 cvxpy 解决方案是否发生变化会很有趣。
我有一个简单的凸问题,我正在尝试加速解决。我正在求解
的 argmin (theta)其中 theta 和 rt 是 Nx1.
我可以用 cvxpy 轻松解决这个问题
import numpy as np
from scipy.optimize import minimize
import cvxpy
np.random.seed(123)
T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))
cvtheta = cvxpy.Variable(N)
fn = -sum([cvxpy.log(1 + cvtheta.T * rt) for rt in R])
prob = cvxpy.Problem(cvxpy.Minimize(fn))
prob.solve()
prob.status
#'optimal'
prob.value
# -5.658335088091929
cvtheta.value
# matrix([[-0.82105079],
# [-0.35475695],
# [-0.41984643],
# [ 0.66117397],
# [ 0.46065358]])
但是对于更大的 R 这变得太慢了,所以我正在尝试使用 scipy 的 fmin_cg:
goalfun 是一个 scipy.minimize 友好的函数,returns 函数值和梯度。
def goalfun(theta, *args):
R = args[0]
N = R.shape[1]
common = (1 + np.sum(theta * R, axis=1))**-1
if np.any( common < 0 ):
return 1e2, 1e2 * np.ones(N)
fun = np.sum(np.log(common))
thetaprime = np.tile(theta, (N, 1)).T
np.fill_diagonal(thetaprime, np.ones(N))
grad = np.sum(np.dot(R, thetaprime) * common[:, None], axis=0)
return fun, grad
确保函数和梯度正确:
goalfun(np.squeeze(np.asarray(cvtheta.value)), R)
# (-5.6583350819293603,
# array([ -9.12423065e-09, -3.36854633e-09, -1.00983679e-08,
# -1.49619901e-08, -1.22987872e-08]))
但是解决这个问题只会产生垃圾,而不管 method、迭代等等。(唯一会产生 Optimization terminated successfully 的是如果 x0 实际上等于最优 θ)
x0 = np.random.rand(R.shape[1])
minimize(fun=goalfun, x0=x0, args=R, jac=True, method='CG')
# fun: 3.3690101669818775
# jac: array([-11.07449021, -14.04017873, -13.38560561, -5.60375334, -2.89210078])
# message: 'Desired error not necessarily achieved due to precision loss.'
# nfev: 25
# nit: 1
# njev: 13
# status: 2
# success: False
# x: array([ 0.00892177, 0.24404118, 0.51627475, 0.21119326, -0.00831957])
即cvxpy 轻松处理的这个看似无害的问题,对于非凸求解器来说完全是病态的。这个问题真的那么讨厌,还是我遗漏了什么?有什么替代方法可以加快速度?
我认为问题在于 theta 可能会使 log 论点变成否定的。看来您已经确定了这个问题,并且在这种情况下 goalfun return 元组 (100,100*ones(N)) 显然是一种启发式尝试,建议求解器认为此 "solution" 是不是 可取的 。但是,必须施加更强的条件,即 "solution" 不 可行 。当然,这可以通过提供适当的约束来完成。 (有趣的是,cvxpy 似乎可以自动处理这个问题。)
这是一个示例 运行,无需提供衍生工具。注意使用可行的初始估计 x0.
np.random.seed(123)
T = 50
N = 5
R = np.random.uniform(-1, 1, size=(T, N))
def goalfun(theta, *args):
R = args[0]
N = R.shape[1]
common = (1 + np.sum(theta * R, axis=1))**-1
return np.sum(np.log(common))
def con_fun(theta, *args):
R = args[0]
return 1+np.sum(theta * R, axis=1)
cons = ({'type': 'ineq', 'fun': lambda x: con_fun(x, R)})
x0 = np.zeros(R.shape[1])
minimize(fun=goalfun, x0=x0, args=R, constraints=cons)
fun: -5.658334806882614 jac: array([ 0.0019, -0.0004, -0.0003, 0.0005, -0.0015, 0. ]) message: 'Optimization terminated successfully.' nfev: 92 nit: 12 njev: 12 status: 0 success: True x: array([-0.8209, -0.3547, -0.4198, 0.6612, 0.4605])
请注意,当我 运行 这样做时,我收到 invalid value encountered in log 警告,表明在搜索的某个时刻检查了 theta 的值,该值几乎不满足约束条件。但是,结果与 cvxpy 的结果相当接近。当在 cvxpy.Problem 公式中明确施加约束时,检查 cvxpy 解决方案是否发生变化会很有趣。