概率不等时桶排序的期望值
expected value in bucket sort when the probability is unequal
我需要帮助来解决与桶排序算法相关的问题,我们有 n 个输入和 n 个桶。我从书中得到的例子显示了一个问题,即一个项目落入某个桶的概率等于 = 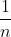 。
。
现在,我发现一个问题,我们有 n 个桶,我们随机生成 n 个数字(范围 0 - 1)。如果生成的数字 y >0.5,我们就掷硬币。如果硬币出现 'HEAD',则 y=y-0.5。
问题是:
- 一个数字 y 落入第一个桶的概率是多少?
- 一个数字 y 落入最后一个桶的概率是多少?
- 如何计算期望值得到这个桶排序的平均运行时间?
谢谢。
- 以概率1/2,y小于1/2;以此为条件,以2/n的概率落入第一个桶。
以概率1 / 2,y大于1/2;以此为条件,落入第一个桶的概率为(1 / 2) (2 / n)。
由全概率定理,概率为1.5 / n。通过对称性,前半部分桶中的每一个都是如此。
由于前半部分桶的概率为 1.5 / n,因此根据对称性,后半部分桶的概率为 (1 - (n / 2)(1.5 / n)) / (0.5n) = 0.5 / n。
期望是线性的。根据期望的线性,期望是对每个桶进行(二次)排序的时间期望的总和。第一个和半个桶中的每一个都有恒定的预期时间。证明与经典桶排序基本相同:每个桶的分布是伯努利分布,参数为 α / n 对于某些 α.
我需要帮助来解决与桶排序算法相关的问题,我们有 n 个输入和 n 个桶。我从书中得到的例子显示了一个问题,即一个项目落入某个桶的概率等于 = 。
现在,我发现一个问题,我们有 n 个桶,我们随机生成 n 个数字(范围 0 - 1)。如果生成的数字 y >0.5,我们就掷硬币。如果硬币出现 'HEAD',则 y=y-0.5。
问题是:
- 一个数字 y 落入第一个桶的概率是多少?
- 一个数字 y 落入最后一个桶的概率是多少?
- 如何计算期望值得到这个桶排序的平均运行时间?
谢谢。
- 以概率1/2,y小于1/2;以此为条件,以2/n的概率落入第一个桶。
以概率1 / 2,y大于1/2;以此为条件,落入第一个桶的概率为(1 / 2) (2 / n)。
由全概率定理,概率为1.5 / n。通过对称性,前半部分桶中的每一个都是如此。
由于前半部分桶的概率为 1.5 / n,因此根据对称性,后半部分桶的概率为 (1 - (n / 2)(1.5 / n)) / (0.5n) = 0.5 / n。
期望是线性的。根据期望的线性,期望是对每个桶进行(二次)排序的时间期望的总和。第一个和半个桶中的每一个都有恒定的预期时间。证明与经典桶排序基本相同:每个桶的分布是伯努利分布,参数为 α / n 对于某些 α.