每对观测值的马氏距离
Mahalanobis distance of each pair of observations
我正在尝试计算数据集 dat 的每个观测值之间的马氏距离,其中每一行都是一个观测值,每一列都是一个变量。这样的距离定义为:
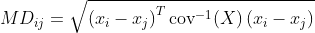
我写了一个函数来做这件事,但我觉得它很慢。有没有更好的方法在 R 中计算这个?
生成一些数据来测试函数:
generateData <- function(nObs, nVar){
library(MASS)
mvrnorm(n=nObs, rep(0,nVar), diag(nVar))
}
这是我目前写的函数。它们都有效,对于我的数据(800 个观测值和 90 个变量),method = "forLoop" 和 method = "apply" 分别需要大约 30 秒和 33 秒。
mhbd_calc2 <- function(dat, method) { #Method is either "forLoop" or "apply"
dat <- as.matrix(na.omit(dat))
nObs <- nrow(dat)
mhbd <- matrix(nrow=nObs,ncol = nObs)
cv_mat_inv = solve(var(dat))
distMH = function(x){ #Mahalanobis distance function
diff = dat[x[1],]-dat[x[2],]
diff %*% cv_mat_inv %*% diff
}
if(method=="forLoop")
{
for (i in 1:nObs){
for(j in 1:i){
mhbd[i,j] <- distMH(c(i,j))
}
}
}
if(method=="apply")
{
mhbd[lower.tri(mhbd)] = apply(combn(nrow(dat),2),2, distMH)
}
result = sqrt(mhbd)
colnames(result)=rownames(dat)
rownames(result)=rownames(dat)
return(as.dist(result))
}
注意:我尝试使用 outer(),但速度更慢(60 秒)
你需要一些数学知识。
- 对经验协方差进行 Cholesky 分解,然后标准化您的观察结果;
- 使用
dist 计算变换观测值的欧氏距离。
dist.maha <- function (dat) {
X <- as.matrix(na.omit(dat)) ## ensure a valid matrix
V <- cov(X) ## empirical covariance; positive definite
L <- t(chol(V)) ## lower triangular factor
stdX <- t(forwardsolve(L, t(X))) ## standardization
dist(stdX) ## use `dist`
}
例子
set.seed(0)
x <- matrix(rnorm(6 * 3), 6, 3)
dist.maha(x)
# 1 2 3 4 5
#2 2.362109
#3 1.725084 1.495655
#4 2.959946 2.715641 2.690788
#5 3.044610 1.218184 1.531026 2.717390
#6 2.740958 1.694767 2.877993 2.978265 2.794879
结果与你的一致mhbd_calc2。
我正在尝试计算数据集 dat 的每个观测值之间的马氏距离,其中每一行都是一个观测值,每一列都是一个变量。这样的距离定义为:
我写了一个函数来做这件事,但我觉得它很慢。有没有更好的方法在 R 中计算这个?
生成一些数据来测试函数:
generateData <- function(nObs, nVar){
library(MASS)
mvrnorm(n=nObs, rep(0,nVar), diag(nVar))
}
这是我目前写的函数。它们都有效,对于我的数据(800 个观测值和 90 个变量),method = "forLoop" 和 method = "apply" 分别需要大约 30 秒和 33 秒。
mhbd_calc2 <- function(dat, method) { #Method is either "forLoop" or "apply"
dat <- as.matrix(na.omit(dat))
nObs <- nrow(dat)
mhbd <- matrix(nrow=nObs,ncol = nObs)
cv_mat_inv = solve(var(dat))
distMH = function(x){ #Mahalanobis distance function
diff = dat[x[1],]-dat[x[2],]
diff %*% cv_mat_inv %*% diff
}
if(method=="forLoop")
{
for (i in 1:nObs){
for(j in 1:i){
mhbd[i,j] <- distMH(c(i,j))
}
}
}
if(method=="apply")
{
mhbd[lower.tri(mhbd)] = apply(combn(nrow(dat),2),2, distMH)
}
result = sqrt(mhbd)
colnames(result)=rownames(dat)
rownames(result)=rownames(dat)
return(as.dist(result))
}
注意:我尝试使用 outer(),但速度更慢(60 秒)
你需要一些数学知识。
- 对经验协方差进行 Cholesky 分解,然后标准化您的观察结果;
- 使用
dist计算变换观测值的欧氏距离。
dist.maha <- function (dat) {
X <- as.matrix(na.omit(dat)) ## ensure a valid matrix
V <- cov(X) ## empirical covariance; positive definite
L <- t(chol(V)) ## lower triangular factor
stdX <- t(forwardsolve(L, t(X))) ## standardization
dist(stdX) ## use `dist`
}
例子
set.seed(0)
x <- matrix(rnorm(6 * 3), 6, 3)
dist.maha(x)
# 1 2 3 4 5
#2 2.362109
#3 1.725084 1.495655
#4 2.959946 2.715641 2.690788
#5 3.044610 1.218184 1.531026 2.717390
#6 2.740958 1.694767 2.877993 2.978265 2.794879
结果与你的一致mhbd_calc2。