MATLAB - 在没有工具箱的情况下拟合指数曲线
MATLAB - Fit exponential curve WITHOUT toolbox
我想对绘制的数据拟合衰减指数。我没有曲线拟合或优化工具箱。
x = [0 0.0036 0.0071 0.0107 0.0143 0.0178 0.0214 0.0250 0.0285 0.0321 0.0357 0.0392 0.0428 0.0464 0.0464];
y = [1.3985 1.3310 1.2741 1.2175 1.1694 1.1213 1.0804 1.0395 1.0043 0.9691 0.9385 0.9080 0.8809 0.7856 0.7856];
figure()
plot(x,y,'*')
如何在 MATLAB 中实现这一点？
假设你在输入点和输出点之间有高斯分布的误差，并且假设误差是加性的，你可以通过经典least squares来解决这个问题。它归结为具有超定线性方程组，其中每个约束定义一个 input-output 观察。以最少的残留误差解决这个超定线性系统就是您正在寻找的解决方案。
警告
Jubobs 在下面给我的评论中提出了一个非常有趣的观点。最小化此残差的参数通常不会最小化原始问题的残差。这个线性化步骤使我们能够以更简单的方式求解参数，但这不是等价问题。然而，由于解决方案足够好，它通常在实践中被接受。
为了将其纳入线性系统，我们需要进行一些巧妙的重新排列。因为要用指数模型拟合一系列点，所以输入x和输出y的关系是：
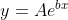
为了得到"linear"，我们可以取两边的自然对数：
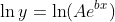
利用 ln(ab) = ln(a) + ln(b) 这一事实，我们有：
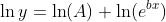
也知道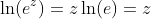
，这简化为：
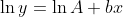
如您所见，上面的等式现在是 "linear" 相对于 log-space。给定一堆 x 和 y 值，所以 (x_1, x_2, ..., x_n) 和 (y_1, y_2, ..., y_n)，我们可以在线性系统中将一堆方程连接在一起：
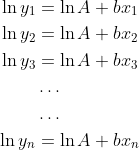
如果我们让 ln(A) = A' 以便于标记，并重新排列它使其成为矩阵形式，我们得到：
因此，我们只需要解决A'和b，你可以通过pseudoinverse来解决。具体来说，上述问题的形式为：
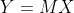
因此，我们需要求解X，所以：
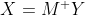
M^{+} 是矩阵的伪逆。完成后，只需在 A' 上使用 exp 运算符即可获得原始 A。 MATLAB 具有非常高效的线性系统求解器和 least-squares 求解器。具体来说，您可以使用 \ 或 ldivide 运算符。您所要做的就是从 x 值创建 M 矩阵，创建 y 值的向量并求解您的系统。真的很简单：
x = ...; %// Define numbers here - either row or column vectors
y = ...;
M = [ones(numel(x),1), x(:)]; %// Ensure x is a column vector
lny = log(y(:)); %// Ensure y is a column vector and take ln
X = M \ lny; %// Solve for parameters
A = exp(X(1)); %// Solve for A
b = X(2); %// Get b
因此，使用您的 x 和 y 值，这就是我得到的：
A =
1.3882
b =
-11.508
如果我们绘制上述点以及拟合直线的指数曲线，我们可以：
xval = linspace(min(x), max(x));
yval = A*exp(b*xval);
plot(x,y,'r.',xval,yval,'b');
第一行代码定义了一组 x 值，这些值介于我们数据集的最小和最大 x 值之间。对于下一行，我们然后通过我们的指数模型获取 x 值和 运行 它们。最后，我们将原始数据点以及通过上述过程找到的参数的指数曲线一起绘制。点是红色的，线是蓝色的。
我们得到：
我觉得挺好看的！对于那些注意到的人来说，上面的图看起来与 MATLAB 生成的普通图和图形 window 有点不同。该图是在 Octave 中生成的，因为我目前正在使用的计算机上没有 MATLAB。但是，上面的代码在 MATLAB 中应该仍然有效。
对于像我这样比较笨的人来说，整个代码（感谢 rayryeng）是：
x = [0 0.0036 0.0071 0.0107 0.0143 0.0178 0.0214 0.0250 0.0285 0.0321 0.0357 0.0392 0.0428 0.0464 0.0464];
y = [1.3985 1.3310 1.2741 1.2175 1.1694 1.1213 1.0804 1.0395 1.0043 0.9691 0.9385 0.9080 0.8809 0.7856 0.7856];
M = [ones(numel(x),1), x(:)]; %// Ensure x is a column vector
lny = log(y(:)); %// Ensure y is a column vector and take ln
X = M\lny; %// Solve for parameters
A = exp(X(1)); %// Solve for A
b = X(2); %// Get b
xval = linspace(min(x), max(x));
yval = A*exp(b*xval);
plot(x,y,'r.',xval,yval,'b');
我想对绘制的数据拟合衰减指数。我没有曲线拟合或优化工具箱。
x = [0 0.0036 0.0071 0.0107 0.0143 0.0178 0.0214 0.0250 0.0285 0.0321 0.0357 0.0392 0.0428 0.0464 0.0464];
y = [1.3985 1.3310 1.2741 1.2175 1.1694 1.1213 1.0804 1.0395 1.0043 0.9691 0.9385 0.9080 0.8809 0.7856 0.7856];
figure()
plot(x,y,'*')
如何在 MATLAB 中实现这一点？
假设你在输入点和输出点之间有高斯分布的误差，并且假设误差是加性的，你可以通过经典least squares来解决这个问题。它归结为具有超定线性方程组，其中每个约束定义一个 input-output 观察。以最少的残留误差解决这个超定线性系统就是您正在寻找的解决方案。
警告
Jubobs 在下面给我的评论中提出了一个非常有趣的观点。最小化此残差的参数通常不会最小化原始问题的残差。这个线性化步骤使我们能够以更简单的方式求解参数，但这不是等价问题。然而，由于解决方案足够好，它通常在实践中被接受。
为了将其纳入线性系统，我们需要进行一些巧妙的重新排列。因为要用指数模型拟合一系列点，所以输入x和输出y的关系是：
为了得到"linear"，我们可以取两边的自然对数：
利用 ln(ab) = ln(a) + ln(b) 这一事实，我们有：
也知道，这简化为：
如您所见，上面的等式现在是 "linear" 相对于 log-space。给定一堆 x 和 y 值，所以 (x_1, x_2, ..., x_n) 和 (y_1, y_2, ..., y_n)，我们可以在线性系统中将一堆方程连接在一起：
如果我们让 ln(A) = A' 以便于标记，并重新排列它使其成为矩阵形式，我们得到：
因此，我们只需要解决A'和b，你可以通过pseudoinverse来解决。具体来说，上述问题的形式为：
因此，我们需要求解X，所以：
M^{+} 是矩阵的伪逆。完成后，只需在 A' 上使用 exp 运算符即可获得原始 A。 MATLAB 具有非常高效的线性系统求解器和 least-squares 求解器。具体来说，您可以使用 \ 或 ldivide 运算符。您所要做的就是从 x 值创建 M 矩阵，创建 y 值的向量并求解您的系统。真的很简单：
x = ...; %// Define numbers here - either row or column vectors
y = ...;
M = [ones(numel(x),1), x(:)]; %// Ensure x is a column vector
lny = log(y(:)); %// Ensure y is a column vector and take ln
X = M \ lny; %// Solve for parameters
A = exp(X(1)); %// Solve for A
b = X(2); %// Get b
因此，使用您的 x 和 y 值，这就是我得到的：
A =
1.3882
b =
-11.508
如果我们绘制上述点以及拟合直线的指数曲线，我们可以：
xval = linspace(min(x), max(x));
yval = A*exp(b*xval);
plot(x,y,'r.',xval,yval,'b');
第一行代码定义了一组 x 值，这些值介于我们数据集的最小和最大 x 值之间。对于下一行，我们然后通过我们的指数模型获取 x 值和 运行 它们。最后，我们将原始数据点以及通过上述过程找到的参数的指数曲线一起绘制。点是红色的，线是蓝色的。
我们得到：
我觉得挺好看的！对于那些注意到的人来说，上面的图看起来与 MATLAB 生成的普通图和图形 window 有点不同。该图是在 Octave 中生成的，因为我目前正在使用的计算机上没有 MATLAB。但是，上面的代码在 MATLAB 中应该仍然有效。
对于像我这样比较笨的人来说，整个代码（感谢 rayryeng）是：
x = [0 0.0036 0.0071 0.0107 0.0143 0.0178 0.0214 0.0250 0.0285 0.0321 0.0357 0.0392 0.0428 0.0464 0.0464];
y = [1.3985 1.3310 1.2741 1.2175 1.1694 1.1213 1.0804 1.0395 1.0043 0.9691 0.9385 0.9080 0.8809 0.7856 0.7856];
M = [ones(numel(x),1), x(:)]; %// Ensure x is a column vector
lny = log(y(:)); %// Ensure y is a column vector and take ln
X = M\lny; %// Solve for parameters
A = exp(X(1)); %// Solve for A
b = X(2); %// Get b
xval = linspace(min(x), max(x));
yval = A*exp(b*xval);
plot(x,y,'r.',xval,yval,'b');