如何集成一个复杂的(不是在真实的 vs 复杂的定义中)功能
How to integrate a complex (not in the real vs complex definition) function
我有一个关于球体周围压力分布的怪物表达式,表达式是
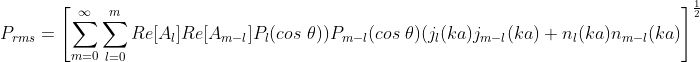 其中 Re[A] 是预定义系数的实部,P 是勒让德多项式,j 和 n 是球形贝塞尔函数和诺依曼函数。
我希望在 theta 上积分,所以我为上面的等式定义了一个函数,如下所示
其中 Re[A] 是预定义系数的实部,P 是勒让德多项式,j 和 n 是球形贝塞尔函数和诺依曼函数。
我希望在 theta 上积分,所以我为上面的等式定义了一个函数,如下所示
def P_rms_calc(k,a,n_max,theta): # Return the P_rms function
# Obtain Coefficients
A_m = A_m_coeff(k,a,P_a,l,z0,n_max)
P_t = []
for m in range(n_max):
for l in range(m+1):
P_t.append(0.5*numpy.real(A_m[l])*numpy.real(A_m[m-l])*(legendre(l)(numpy.cos(theta)))*(legendre(m-l)(numpy.cos(theta)))*((spherical_jn(l,k*r)*spherical_jn(m-l,k*r))+
(spherical_yn(l,k*r)*spherical_yn(m-l,k*r))))
P_rms = numpy.sqrt(sum(P_t))
return P_rms
但是,当我尝试像这样使用 scipy.integrate.quad 进行集成时,
a0, err = quad(P_rms_calc(k,a,n_max,theta),-numpy.pi,numpy.pi)
它给出 'error: quad: first argument is not callable'。如果我不这样给出函数的参数,
a0, err = (1/(2*numpy.pi))*quad(P_rms_calc,-numpy.pi,numpy.pi)
它给出 'TypeError: P_rms_calc() takes exactly 8 arguments (1 given)'
我在使用集成工具 quad 时是否遗漏了一些简单的东西?如果没有,有没有更好的方法来尝试整合这个表达式?您也可以随意推荐一种更有效的方法来定义均方根压力表达式。作为参考,我只是从 m=0 到 6 左右求和,所以使用 for loops.Thanks 的帮助计算时间并不可怕!
使用args参数传递被积函数的额外参数:
>>> def func(x, a, b):
... return a * x**b
...
>>> quad(func, 0, 1, args=(1., 2.))
(0.33333333333333337, 3.700743415417189e-15)
我有一个关于球体周围压力分布的怪物表达式,表达式是
其中 Re[A] 是预定义系数的实部,P 是勒让德多项式,j 和 n 是球形贝塞尔函数和诺依曼函数。
我希望在 theta 上积分,所以我为上面的等式定义了一个函数,如下所示
def P_rms_calc(k,a,n_max,theta): # Return the P_rms function
# Obtain Coefficients
A_m = A_m_coeff(k,a,P_a,l,z0,n_max)
P_t = []
for m in range(n_max):
for l in range(m+1):
P_t.append(0.5*numpy.real(A_m[l])*numpy.real(A_m[m-l])*(legendre(l)(numpy.cos(theta)))*(legendre(m-l)(numpy.cos(theta)))*((spherical_jn(l,k*r)*spherical_jn(m-l,k*r))+
(spherical_yn(l,k*r)*spherical_yn(m-l,k*r))))
P_rms = numpy.sqrt(sum(P_t))
return P_rms
但是,当我尝试像这样使用 scipy.integrate.quad 进行集成时,
a0, err = quad(P_rms_calc(k,a,n_max,theta),-numpy.pi,numpy.pi)
它给出 'error: quad: first argument is not callable'。如果我不这样给出函数的参数,
a0, err = (1/(2*numpy.pi))*quad(P_rms_calc,-numpy.pi,numpy.pi)
它给出 'TypeError: P_rms_calc() takes exactly 8 arguments (1 given)'
我在使用集成工具 quad 时是否遗漏了一些简单的东西?如果没有,有没有更好的方法来尝试整合这个表达式?您也可以随意推荐一种更有效的方法来定义均方根压力表达式。作为参考,我只是从 m=0 到 6 左右求和,所以使用 for loops.Thanks 的帮助计算时间并不可怕!
使用args参数传递被积函数的额外参数:
>>> def func(x, a, b):
... return a * x**b
...
>>> quad(func, 0, 1, args=(1., 2.))
(0.33333333333333337, 3.700743415417189e-15)