在求解 2*2 实矩阵的特征向量时阐明机器 epsilon 的影响
Clarify effects of machine epsilon when solving for eigenvectors of a 2*2 real matrix
代码来自opencv中的函数eigen2x2。
对于具有以下形式的实数矩阵:

求解其特征值:
double u = (a + c)*0.5;
double v = std::sqrt((a - c)*(a - c)*0.25 + b*b);
double l1 = u + v; //the 1st eigenvalue
double l2 = u - v; // the 2nd eigenvalue
然后求解l1对应的特征向量,即求解如下系统:
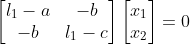
eigen2x2中的代码如下:
double x = b;
double y = l1 - a;
double e = fabs(x);
if (e + fabs(y) < 1e-4)
{
y = b;
x = l1 - c;
e = fabs(x);
if (e + fabs(y) < 1e-4)
{
e = 1. / (e + fabs(y) + FLT_EPSILON);
x *= e, y *= e;
}
}
double d = 1. / std::sqrt(x*x + y*y + DBL_EPSILON);
double x1 = x*d; //I moderately changed variable name for simplicity.
double x2 = y*d;
其中x1和x2构成l1对应的特征向量。
问题
据我了解,当矩阵逼近零矩阵时,将执行以下代码:
e = 1. / (e + fabs(y) + FLT_EPSILON);
x *= e, y *= e;
那么它的作用是什么呢?是否允许踢出 FLT_EPSILON 和随后的 DBL_EPSILON?
它们的存在是为了防止除以零(或亚 epsilon 值)。相反,你会得到一个大的浮点数。
假设您的值大小适中,它应该对结果几乎没有影响;比其他舍入效果更小。
安全地删除它需要一些子集来编写大量的单元测试,找到记录的案例为什么最初添加它,或者在各种各样的实时代码中广泛使用,在这些代码中,不良行为是安全的(没有金钱声誉或生活在线)但很明显。单元测试需要覆盖一系列小的、零的、非规范化的值与中值和大值的混合,包括白盒逆向工程以在每个中间步骤生成所述值(安全起见)。
我会把它们留在里面;他们看起来无害。
代码来自opencv中的函数eigen2x2。
对于具有以下形式的实数矩阵:
求解其特征值:
double u = (a + c)*0.5;
double v = std::sqrt((a - c)*(a - c)*0.25 + b*b);
double l1 = u + v; //the 1st eigenvalue
double l2 = u - v; // the 2nd eigenvalue
然后求解l1对应的特征向量,即求解如下系统:
eigen2x2中的代码如下:
double x = b;
double y = l1 - a;
double e = fabs(x);
if (e + fabs(y) < 1e-4)
{
y = b;
x = l1 - c;
e = fabs(x);
if (e + fabs(y) < 1e-4)
{
e = 1. / (e + fabs(y) + FLT_EPSILON);
x *= e, y *= e;
}
}
double d = 1. / std::sqrt(x*x + y*y + DBL_EPSILON);
double x1 = x*d; //I moderately changed variable name for simplicity.
double x2 = y*d;
其中x1和x2构成l1对应的特征向量。
问题
据我了解,当矩阵逼近零矩阵时,将执行以下代码:
e = 1. / (e + fabs(y) + FLT_EPSILON);
x *= e, y *= e;
那么它的作用是什么呢?是否允许踢出 FLT_EPSILON 和随后的 DBL_EPSILON?
它们的存在是为了防止除以零(或亚 epsilon 值)。相反,你会得到一个大的浮点数。
假设您的值大小适中,它应该对结果几乎没有影响;比其他舍入效果更小。
安全地删除它需要一些子集来编写大量的单元测试,找到记录的案例为什么最初添加它,或者在各种各样的实时代码中广泛使用,在这些代码中,不良行为是安全的(没有金钱声誉或生活在线)但很明显。单元测试需要覆盖一系列小的、零的、非规范化的值与中值和大值的混合,包括白盒逆向工程以在每个中间步骤生成所述值(安全起见)。
我会把它们留在里面;他们看起来无害。