如果根据指数分布，2 分钟内到达车站的人数超过 100 人的概率是多少？
What is the probability of more than 100 people arriving at the station, if they come based on exponential distribution with 2 mins?
所以，我遇到了这个问题：
“人们根据指数分布到达公交车站。
你知道分布的均值是 2 分钟。
3 小时内超过 100 人到达的概率是多少。
所以我发现问题是，我们必须计算实际平均值低于 1.8 分钟的概率。
但我真的不知道如何解决这个问题？
它有置信区间吗？
所以基本上，在 3 小时内吸引 100 位客户的到达率将为每位客户 1.8 分钟。使用累积分布函数：
这里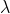 
= 0.5 且 t = 1.8。由于我们正在寻找3小时内超过100位客户，因此积分将从0到1.8。
这给出了 1-e^(-0.5*1.8) 你的答案，即 0.5934。
You can refer this link to get hold on the theory and few examples.
所以，我遇到了这个问题： “人们根据指数分布到达公交车站。 你知道分布的均值是 2 分钟。
3 小时内超过 100 人到达的概率是多少。
所以我发现问题是，我们必须计算实际平均值低于 1.8 分钟的概率。
但我真的不知道如何解决这个问题？ 它有置信区间吗？
所以基本上，在 3 小时内吸引 100 位客户的到达率将为每位客户 1.8 分钟。使用累积分布函数：
这里 = 0.5 且 t = 1.8。由于我们正在寻找3小时内超过100位客户，因此积分将从0到1.8。
这给出了 1-e^(-0.5*1.8) 你的答案，即 0.5934。
You can refer this link to get hold on the theory and few examples.