求解线性方程组
Solving a linear system of equations
我正在研究使用有限元法来计算通过元件的热流。
我目前正在解决一个方程组,其中等式两边都有变量。一个简单的例子可能是这样的
| 1 -1 0| |100 | |q1|
|-1 2 -1| . | T2 | = |0 |
| 0 -1 1| | 0 | |q3|
我正在考虑使用的方法会将矩阵缩小为 2x2,因为温度 "T1" 已知,并相应地更改右侧。并继续在 "T3" 的行中执行相同的操作。
但是我的辅导员一直建议我反对这个。
你会如何解决这样的系统?
我会写下你的线性方程并重塑它,这样你只有一个带有未知变量的向量。例如,上面的方程式系统等于:
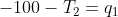
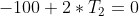
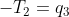
可重写:
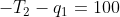
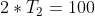
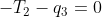
产生:
| -1 -1 0| | T2 | | 100 |
| 2 0 0| . | q1 | = | 100 |
| -1 0 -1| | q3 | | 0 |
另一种方法是创建一个置换矩阵以从向量中提取已知和未知行。
这种方法有点复杂,但对程序员更友好:
说出你的情商。系统是:
K . T = Q
其中 K 是 3x3,T 和 Q 是 3x1 向量。您可以创建一个置换 Pf 矩阵,当它乘以 T 时,结果是 T 矩阵的未知部分(仅 T2),在您的情况下,置换矩阵将是一个 1x3 矩阵:
Pf = [0 1 0]
|100|
Tf = Pf * T = [0 1 0]* |T2 | = [T2]
|0 |
另一个置换矩阵将从 T 矩阵中获取已知部分,在您的情况下它将是 2x3 矩阵:
| 1 0 0|
Ps = | 0 0 1|
Ts = Ps * T = | 1 0 0| |100| |100|
| 0 0 1| *| T2| = |0 |
|0 |
现在一切就绪,你可以假设系统是这样的:
K . T = Q
K = |Kff Kfs|
|Kfs Kss|
Q = |Qf|
|Qs|
T = |Tf|
|Ts|
其中 f 是未知右侧的前缀,s 前缀是已知右侧的前缀。您可以找到 Pf、Ps、Qf、Qs、Kff、Kfs、Ksf 和 Kss像这样:
Tf = Pf * T
Tq = Ps * T
Qf = Pf * Q
Qq = Ps * Q
Kff = pf * K * pf` (note: ` denotes the transpose)
Kfs = pf * K * ps` (note: ` denotes the transpose)
Ksf = ps * K * pf` (note: ` denotes the transpose)
Kss = ps * K * ps` (note: ` denotes the transpose)
现在需要找到未知向量 Tf 和 Qs:
K . T = Q
|Kff Kfs| |Tf| = |Qf|
|Kfs Kss| |Ts| |Qs|
表示:
Kff * Tf + Kfs * Ts = Qf
Kfs * Tf + Kss * Ts = Qs
来自第一个:
Tf = Kff^-1 * (Qf - Kfs * Ts)
用上式可以求出Tf(注意右边都是已知的矩阵和向量,所以需要进行数值运算)
从第二个开始:
Qs = Kfs * Tf + Kss * Ts
这样 Qs 和 Tf 都找到了。一旦你找到 Tf 和 Qs,你可以这样做来形成原始的 T 和 Q 矩阵:
Q = Ps` * Qs + Pf` * Qf
T = Ps` * Ts + Pf` * Tf
我正在研究使用有限元法来计算通过元件的热流。 我目前正在解决一个方程组,其中等式两边都有变量。一个简单的例子可能是这样的
| 1 -1 0| |100 | |q1|
|-1 2 -1| . | T2 | = |0 |
| 0 -1 1| | 0 | |q3|
我正在考虑使用的方法会将矩阵缩小为 2x2,因为温度 "T1" 已知,并相应地更改右侧。并继续在 "T3" 的行中执行相同的操作。 但是我的辅导员一直建议我反对这个。
你会如何解决这样的系统?
我会写下你的线性方程并重塑它,这样你只有一个带有未知变量的向量。例如,上面的方程式系统等于:
可重写:
产生:
| -1 -1 0| | T2 | | 100 |
| 2 0 0| . | q1 | = | 100 |
| -1 0 -1| | q3 | | 0 |
另一种方法是创建一个置换矩阵以从向量中提取已知和未知行。 这种方法有点复杂,但对程序员更友好:
说出你的情商。系统是:
K . T = Q
其中 K 是 3x3,T 和 Q 是 3x1 向量。您可以创建一个置换 Pf 矩阵,当它乘以 T 时,结果是 T 矩阵的未知部分(仅 T2),在您的情况下,置换矩阵将是一个 1x3 矩阵:
Pf = [0 1 0]
|100|
Tf = Pf * T = [0 1 0]* |T2 | = [T2]
|0 |
另一个置换矩阵将从 T 矩阵中获取已知部分,在您的情况下它将是 2x3 矩阵:
| 1 0 0|
Ps = | 0 0 1|
Ts = Ps * T = | 1 0 0| |100| |100|
| 0 0 1| *| T2| = |0 |
|0 |
现在一切就绪,你可以假设系统是这样的:
K . T = Q
K = |Kff Kfs|
|Kfs Kss|
Q = |Qf|
|Qs|
T = |Tf|
|Ts|
其中 f 是未知右侧的前缀,s 前缀是已知右侧的前缀。您可以找到 Pf、Ps、Qf、Qs、Kff、Kfs、Ksf 和 Kss像这样:
Tf = Pf * T
Tq = Ps * T
Qf = Pf * Q
Qq = Ps * Q
Kff = pf * K * pf` (note: ` denotes the transpose)
Kfs = pf * K * ps` (note: ` denotes the transpose)
Ksf = ps * K * pf` (note: ` denotes the transpose)
Kss = ps * K * ps` (note: ` denotes the transpose)
现在需要找到未知向量 Tf 和 Qs:
K . T = Q
|Kff Kfs| |Tf| = |Qf|
|Kfs Kss| |Ts| |Qs|
表示:
Kff * Tf + Kfs * Ts = Qf
Kfs * Tf + Kss * Ts = Qs
来自第一个:
Tf = Kff^-1 * (Qf - Kfs * Ts)
用上式可以求出Tf(注意右边都是已知的矩阵和向量,所以需要进行数值运算)
从第二个开始:
Qs = Kfs * Tf + Kss * Ts
这样 Qs 和 Tf 都找到了。一旦你找到 Tf 和 Qs,你可以这样做来形成原始的 T 和 Q 矩阵:
Q = Ps` * Qs + Pf` * Qf
T = Ps` * Ts + Pf` * Tf