Monte Carlo 在边界点 a 和 b 内积分的 Fortan 代码
Fortan code for Monte Carlo Integration within boundary point a and b
我了解Monte carlo模拟是通过绘制随机点并计算曲线内外点之间的比率来估计面积。
假设曲线半径为1,我已经很好地计算了pi的值。
这是代码
program pi
implicit none
integer :: count, n, i
real :: r, x, y
count = 0
n=500
CALL RANDOM_SEED
DO i = 1, n
CALL RANDOM_NUMBER(x)
CALL RANDOM_NUMBER(y)
IF (x*x + y*Y <1.0) count = count + 1
END DO
r = 4 * REAL(count)/n
print *, r
end program pi
但是要找到整合,教科书说要应用相同的想法。但是如果我想找到
的集成,我不知道如何编写代码
f(x)=sqrt(1+x**2) over a = 1 and b = 5
在半径为一之前,我确实假设点落入条件 x*2+y**2 但我如何解决上面的问题?
任何帮助都非常有帮助
我先写代码再解释:
Program integral
implicit none
real f
integer, parameter:: a=1, b=5, Nmc=10000000 !a the lower bound, b the upper bound, Nmc the size of the sampling (the higher, the more accurate the result)
real:: x, SUM=0
do i=1,Nmc !Starting MC sampling
call RANDOM_NUMBER(x) !generating random number x in range [0,1]
x=a+x*(b-a) !converting x to be in range [a,b]
SUM=SUM+f(x) !summing all values of f(x). EDIT: SUM is also an instrinsic function in Fortran so don't call your variable this, I named it so, to illustrate its purpose
enddo
print*, (b-a)*(SUM/Nmc) !final result of your integral
end program integral
function f(x) !defining your function
implicit none
real, intent(in):: x
real:: f
f=sqrt(1+x**2)
end function f
那么发生了什么:
积分 可以写成
可以写成
 。其中:
。其中:
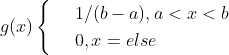
(这个g(x)是变量x在[a,b]中的均匀概率分布)。我们可以将积分写为:
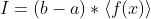
其中  .
.
所以,最后,我们得到积分应该是:
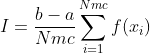
因此,您所要做的就是在 [a,b] 范围内生成一个随机数,然后为这个 x 计算您的函数值。然后重复多次(Nmc 次),计算总和。然后除以 Nmc,求平均值,然后乘以 (b-a)。这就是代码的作用。
互联网上有很多这方面的资料。 here's 一个非常形象化的例子
编辑:第二种方式,与 Pi 方法相同:
Nin=0 !Number of points inside the function (under the curve)
do i=1,Nmc
call random_number(x)
call random_number(y)
x=a+x*(b-a)
y=f_min+y(f_max-f_min)
if (f(x)<y) Nin=Nin+1
enddo
print*, (f_max-f_min)*(b-a)*(real(Nin)/Nmc)
所有这些,然后你可以将它包含在一个外部 do 循环中,总结 (f_max-f_min)(b-a)(real(Nin)/Nmc) 和最后打印其平均值。
对于此示例,您所做的实际上是创建一个从 a 到 b(x 维度)和从 f_min 到 f_max(y 维度)的封闭框,然后对该区域内的点进行采样并计数函数 (Nin) 中的点。显然,您必须知道函数在 [a,b] 范围内的最小值 (f_min) 和最大值 (f_max)。或者你可以为你的 f_min f_max 任意使用 low/high 值,但那样你会浪费很多点,你的错误会更大。
我了解Monte carlo模拟是通过绘制随机点并计算曲线内外点之间的比率来估计面积。
假设曲线半径为1,我已经很好地计算了pi的值。
这是代码
program pi
implicit none
integer :: count, n, i
real :: r, x, y
count = 0
n=500
CALL RANDOM_SEED
DO i = 1, n
CALL RANDOM_NUMBER(x)
CALL RANDOM_NUMBER(y)
IF (x*x + y*Y <1.0) count = count + 1
END DO
r = 4 * REAL(count)/n
print *, r
end program pi
但是要找到整合,教科书说要应用相同的想法。但是如果我想找到
的集成,我不知道如何编写代码f(x)=sqrt(1+x**2) over a = 1 and b = 5
在半径为一之前,我确实假设点落入条件 x*2+y**2 但我如何解决上面的问题?
任何帮助都非常有帮助
我先写代码再解释:
Program integral
implicit none
real f
integer, parameter:: a=1, b=5, Nmc=10000000 !a the lower bound, b the upper bound, Nmc the size of the sampling (the higher, the more accurate the result)
real:: x, SUM=0
do i=1,Nmc !Starting MC sampling
call RANDOM_NUMBER(x) !generating random number x in range [0,1]
x=a+x*(b-a) !converting x to be in range [a,b]
SUM=SUM+f(x) !summing all values of f(x). EDIT: SUM is also an instrinsic function in Fortran so don't call your variable this, I named it so, to illustrate its purpose
enddo
print*, (b-a)*(SUM/Nmc) !final result of your integral
end program integral
function f(x) !defining your function
implicit none
real, intent(in):: x
real:: f
f=sqrt(1+x**2)
end function f
那么发生了什么:
积分可以写成
。其中:
(这个g(x)是变量x在[a,b]中的均匀概率分布)。我们可以将积分写为:
其中 .
所以,最后,我们得到积分应该是:
因此,您所要做的就是在 [a,b] 范围内生成一个随机数,然后为这个 x 计算您的函数值。然后重复多次(Nmc 次),计算总和。然后除以 Nmc,求平均值,然后乘以 (b-a)。这就是代码的作用。
互联网上有很多这方面的资料。 here's 一个非常形象化的例子
编辑:第二种方式,与 Pi 方法相同:
Nin=0 !Number of points inside the function (under the curve)
do i=1,Nmc
call random_number(x)
call random_number(y)
x=a+x*(b-a)
y=f_min+y(f_max-f_min)
if (f(x)<y) Nin=Nin+1
enddo
print*, (f_max-f_min)*(b-a)*(real(Nin)/Nmc)
所有这些,然后你可以将它包含在一个外部 do 循环中,总结 (f_max-f_min)(b-a)(real(Nin)/Nmc) 和最后打印其平均值。 对于此示例,您所做的实际上是创建一个从 a 到 b(x 维度)和从 f_min 到 f_max(y 维度)的封闭框,然后对该区域内的点进行采样并计数函数 (Nin) 中的点。显然,您必须知道函数在 [a,b] 范围内的最小值 (f_min) 和最大值 (f_max)。或者你可以为你的 f_min f_max 任意使用 low/high 值,但那样你会浪费很多点,你的错误会更大。