如何计算两个物体之间的相对位姿并将它们放入变换矩阵
How to calculate relative pose between two objects and put them in a transformation matrix
我有两个物体的姿势。它们是根据 x、y、z 和滚动、俯仰和偏航（我将它们放在四元数中，然后将它们转换为滚动、俯仰、偏航）。我需要做的是记录两个物体之间的相对姿势，记录它们，这样，当其中一个物体旋转时，另一个物体也会以完全相同的方式平移和旋转。我从物体的质心获取姿势。
此视频将说明我打算做什么。
https://drive.google.com/file/d/1NKtS9fv-FasloVwCKqYIAV1Uc2i9_PN0/view
我访问了以下站点寻求帮助：
http://planning.cs.uiuc.edu/node102.html
请帮助我，我被困了很长时间，我需要一个方向，我是机器人学的新手，我没有任何计算机视觉背景。
@Vik，所以我已经按照你想要的方式实现了，但是它不能正常工作。我在 python 的 ROS 环境中工作，但我已经给出了代码的逻辑部分。如果你能看一看，那将是非常有帮助的。我从这里得到了我的矩阵：http://planning.cs.uiuc.edu/node104.html
#This is object2
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = 0.90
p.pose.position.y = 0.30
p.pose.position.z = 1.2
p.pose.orientation.x=0.0
p.pose.orientation.y=0.0
p.pose.orientation.z=0.0
p.pose.orientation.w=1.0
scene.add_box("object2", p, (0.1, 0.1, 0.2))
rospy.sleep(2)
quaternion1 = (p.pose.orientation.x,p.pose.orientation.y,p.pose.orientation.z,p.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion1, axes='sxyz') # will provide result in x, y,z sequence
roll=euler[0]
pitch=euler[1]
yaw=euler[2]
C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p.pose.position.z
C30=0
C31=0
C32=0
C33=1
obj2_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])
#This is object1
p1 = PoseStamped()
p1.header.frame_id = robot.get_planning_frame()
p1.pose.position.x = 0.9
p1.pose.position.y = 0.30
p1.pose.position.z = 0.7
p1.pose.orientation.x=0.0
p1.pose.orientation.y=0.0
p1.pose.orientation.z=0.0
p1.pose.orientation.w=1.0
scene.add_box("object1", p1, (0.1, 0.1, 0.5))
rospy.sleep(2)
quaternion2 = (p1.pose.orientation.x,p1.pose.orientation.y,p1.pose.orientation.z,p1.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion2, axes='sxyz')
roll=euler[0]
pitch=euler[1]
yaw=euler[2]
C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p1.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p1.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p1.pose.position.z
C30=0
C31=0
C32=0
C33=1
obj1_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])
transformation_mat=np.dot(inv(obj2_mat), obj1_mat) #generating the transformation
rospy.sleep(10)
#This is object1 in second pose
p2 = PoseStamped()
p2.header.frame_id = robot.get_planning_frame()
p2.pose.position.x = 0.70
p2.pose.position.y = -0.9
p2.pose.position.z = 0.7
p2.pose.orientation.x=0.3826834
p2.pose.orientation.y=0.0
p2.pose.orientation.z=0.0
p2.pose.orientation.w=-0.9238795
scene.add_box("object1", p2, (0.1, 0.1, 0.5))
object_position_mat=np.array([[p2.pose.position.x],[p2.pose.position.y],[p2.pose.position.z],[1]]) # (x,y,z,1) position matrix for object1 in its second position
rospy.sleep(2)
Final_position=np.dot(transformation_mat, object_position_mat) #Getting the new position of object2 by multiplying transformation matrix with position of object1
print "============ Generating plan 2"
#This is object2 in second pose
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = Final_position[0]
p.pose.position.y = Final_position[1]
p.pose.position.z = Final_position[2]
p.pose.orientation.x=p2.pose.orientation.x #Kept the same orientation values of object1 in second pose, did not do any calculation as it is logical
p.pose.orientation.y=p2.pose.orientation.y
p.pose.orientation.z=p2.pose.orientation.z
p.pose.orientation.w=p2.pose.orientation.w
scene.add_box("object2", p, (0.1, 0.1, 0.2))
使用 http://www.ccs.neu.edu/home/rplatt/cs5335_fall2017/slides/homogeneous_transforms.pdf 中的符号，假设您有 2 个世界坐标系中对象的齐次变换矩阵
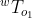和 
.
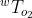您可以使用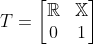 
组成 4x4 变换矩阵，其中 R 是 3x3 旋转矩阵，X 是 3x1 平移向量。
您要查找的是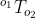 
，它只是 
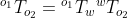，其中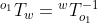 
以您想要的方式转换对象一后，您应该能够直接应用 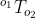并获得想要的结果。
更新：
如果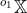
指对象2的局部坐标系中的点坐标（例如对象点，如它的角）为
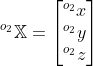。然后这些点在任意帧f中给出为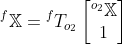
这是一些基于您的代码的代码，希望我能理解您的意图：
from tf.transformations import euler_from_quaternion, quaternion_from_euler, \
quaternion_matrix, quaternion_from_matrix
from geometry_msgs.msg import PoseStamped, Pose, Point, Quaternion
from std_msgs.msg import Header
import numpy as np
def PoseStamped_2_mat(p):
q = p.pose.orientation
pos = p.pose.position
T = quaternion_matrix([q.x,q.y,q.z,q.w])
T[:3,3] = np.array([pos.x,pos.y,pos.z])
return T
def Mat_2_posestamped(m,f_id="test"):
q = quaternion_from_matrix(m)
p = PoseStamped(header = Header(frame_id=f_id), #robot.get_planning_frame()
pose=Pose(position=Point(*m[:3,3]),
orientation=Quaternion(*q)))
return p
def T_inv(T_in):
R_in = T_in[:3,:3]
t_in = T_in[:3,[-1]]
R_out = R_in.T
t_out = -np.matmul(R_out,t_in)
return np.vstack((np.hstack((R_out,t_out)),np.array([0, 0, 0, 1])))
#This is object2
p_o2 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.9,0.3,1.2),
orientation=Quaternion(0,0,0,1)))
#scene.add_box("object2", p_o2, (0.1, 0.1, 0.2))
#rospy.sleep(2)
Tw2 = PoseStamped_2_mat(p_o2)
#This is object1
p_o1 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.9,0.3,0.7),
orientation=Quaternion(0,0,0,1)))
#scene.add_box("object1", p_o1, (0.1, 0.1, 0.5))
#rospy.sleep(2)
Tw1 = PoseStamped_2_mat(p_o1)
T2w = T_inv(Tw2)
T21 = np.matmul(T2w, Tw1)
#rospy.sleep(10)
#This is object1 in second pose
p_o2_prime = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.7,-0.9,0.7),
orientation=Quaternion(0.3826834,0,0,-0.9238795)))
#scene.add_box("object1", p_o2_prime, (0.1, 0.1, 0.5))
Tw2_prime = PoseStamped_2_mat(p_o2_prime)
Tw1_prime = np.matmul(Tw2_prime, T21)
#rospy.sleep(2)
print "============ Generating plan 2"
#This is object2 in second pose
p_o1_prime = Mat_2_posestamped(Tw1_prime, f_id="test") # robot.get_planning_frame()
#scene.add_box("object2", p_o1_prime, (0.1, 0.1, 0.2))
我有两个物体的姿势。它们是根据 x、y、z 和滚动、俯仰和偏航（我将它们放在四元数中，然后将它们转换为滚动、俯仰、偏航）。我需要做的是记录两个物体之间的相对姿势，记录它们，这样，当其中一个物体旋转时，另一个物体也会以完全相同的方式平移和旋转。我从物体的质心获取姿势。
此视频将说明我打算做什么。
https://drive.google.com/file/d/1NKtS9fv-FasloVwCKqYIAV1Uc2i9_PN0/view
我访问了以下站点寻求帮助：
http://planning.cs.uiuc.edu/node102.html
请帮助我，我被困了很长时间，我需要一个方向，我是机器人学的新手，我没有任何计算机视觉背景。
@Vik，所以我已经按照你想要的方式实现了，但是它不能正常工作。我在 python 的 ROS 环境中工作，但我已经给出了代码的逻辑部分。如果你能看一看，那将是非常有帮助的。我从这里得到了我的矩阵：http://planning.cs.uiuc.edu/node104.html
#This is object2
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = 0.90
p.pose.position.y = 0.30
p.pose.position.z = 1.2
p.pose.orientation.x=0.0
p.pose.orientation.y=0.0
p.pose.orientation.z=0.0
p.pose.orientation.w=1.0
scene.add_box("object2", p, (0.1, 0.1, 0.2))
rospy.sleep(2)
quaternion1 = (p.pose.orientation.x,p.pose.orientation.y,p.pose.orientation.z,p.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion1, axes='sxyz') # will provide result in x, y,z sequence
roll=euler[0]
pitch=euler[1]
yaw=euler[2]
C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p.pose.position.z
C30=0
C31=0
C32=0
C33=1
obj2_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])
#This is object1
p1 = PoseStamped()
p1.header.frame_id = robot.get_planning_frame()
p1.pose.position.x = 0.9
p1.pose.position.y = 0.30
p1.pose.position.z = 0.7
p1.pose.orientation.x=0.0
p1.pose.orientation.y=0.0
p1.pose.orientation.z=0.0
p1.pose.orientation.w=1.0
scene.add_box("object1", p1, (0.1, 0.1, 0.5))
rospy.sleep(2)
quaternion2 = (p1.pose.orientation.x,p1.pose.orientation.y,p1.pose.orientation.z,p1.pose.orientation.w)
euler = tf.transformations.euler_from_quaternion(quaternion2, axes='sxyz')
roll=euler[0]
pitch=euler[1]
yaw=euler[2]
C00=math.cos(yaw)*math.cos(pitch)
C01=math.cos(yaw)*math.sin(pitch)*math.sin(roll) - math.sin(yaw)*math.sin(roll)
C02=math.cos(yaw)*math.sin(pitch)*math.cos(roll) + math.sin(yaw)*math.sin(roll)
C03=p1.pose.position.x
C10=math.sin(yaw)*math.cos(pitch)
C11=math.sin(yaw)*math.sin(pitch)*math.sin(roll) + math.cos(yaw)*math.cos(roll)
C12=math.sin(yaw)*math.sin(pitch)*math.cos(roll) -math.cos(yaw)*math.sin(roll)
C13=p1.pose.position.y
C20= -math.sin(pitch)
C21=math.cos(pitch)*math.sin(roll)
C22=math.cos(pitch)*math.cos(roll)
C23=p1.pose.position.z
C30=0
C31=0
C32=0
C33=1
obj1_mat=np.array([[C00, C01, C02, C03],[C10, C11, C12, C13],[C20, C21, C22, C23],[C30, C31, C32, C33]])
transformation_mat=np.dot(inv(obj2_mat), obj1_mat) #generating the transformation
rospy.sleep(10)
#This is object1 in second pose
p2 = PoseStamped()
p2.header.frame_id = robot.get_planning_frame()
p2.pose.position.x = 0.70
p2.pose.position.y = -0.9
p2.pose.position.z = 0.7
p2.pose.orientation.x=0.3826834
p2.pose.orientation.y=0.0
p2.pose.orientation.z=0.0
p2.pose.orientation.w=-0.9238795
scene.add_box("object1", p2, (0.1, 0.1, 0.5))
object_position_mat=np.array([[p2.pose.position.x],[p2.pose.position.y],[p2.pose.position.z],[1]]) # (x,y,z,1) position matrix for object1 in its second position
rospy.sleep(2)
Final_position=np.dot(transformation_mat, object_position_mat) #Getting the new position of object2 by multiplying transformation matrix with position of object1
print "============ Generating plan 2"
#This is object2 in second pose
p = PoseStamped()
p.header.frame_id = robot.get_planning_frame()
p.pose.position.x = Final_position[0]
p.pose.position.y = Final_position[1]
p.pose.position.z = Final_position[2]
p.pose.orientation.x=p2.pose.orientation.x #Kept the same orientation values of object1 in second pose, did not do any calculation as it is logical
p.pose.orientation.y=p2.pose.orientation.y
p.pose.orientation.z=p2.pose.orientation.z
p.pose.orientation.w=p2.pose.orientation.w
scene.add_box("object2", p, (0.1, 0.1, 0.2))
使用 http://www.ccs.neu.edu/home/rplatt/cs5335_fall2017/slides/homogeneous_transforms.pdf 中的符号，假设您有 2 个世界坐标系中对象的齐次变换矩阵
和
.
您可以使用 组成 4x4 变换矩阵，其中 R 是 3x3 旋转矩阵，X 是 3x1 平移向量。
您要查找的是 ，它只是
，其中
以您想要的方式转换对象一后，您应该能够直接应用 并获得想要的结果。
更新：
如果指对象2的局部坐标系中的点坐标（例如对象点，如它的角）为
。然后这些点在任意帧f中给出为
这是一些基于您的代码的代码，希望我能理解您的意图：
from tf.transformations import euler_from_quaternion, quaternion_from_euler, \
quaternion_matrix, quaternion_from_matrix
from geometry_msgs.msg import PoseStamped, Pose, Point, Quaternion
from std_msgs.msg import Header
import numpy as np
def PoseStamped_2_mat(p):
q = p.pose.orientation
pos = p.pose.position
T = quaternion_matrix([q.x,q.y,q.z,q.w])
T[:3,3] = np.array([pos.x,pos.y,pos.z])
return T
def Mat_2_posestamped(m,f_id="test"):
q = quaternion_from_matrix(m)
p = PoseStamped(header = Header(frame_id=f_id), #robot.get_planning_frame()
pose=Pose(position=Point(*m[:3,3]),
orientation=Quaternion(*q)))
return p
def T_inv(T_in):
R_in = T_in[:3,:3]
t_in = T_in[:3,[-1]]
R_out = R_in.T
t_out = -np.matmul(R_out,t_in)
return np.vstack((np.hstack((R_out,t_out)),np.array([0, 0, 0, 1])))
#This is object2
p_o2 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.9,0.3,1.2),
orientation=Quaternion(0,0,0,1)))
#scene.add_box("object2", p_o2, (0.1, 0.1, 0.2))
#rospy.sleep(2)
Tw2 = PoseStamped_2_mat(p_o2)
#This is object1
p_o1 = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.9,0.3,0.7),
orientation=Quaternion(0,0,0,1)))
#scene.add_box("object1", p_o1, (0.1, 0.1, 0.5))
#rospy.sleep(2)
Tw1 = PoseStamped_2_mat(p_o1)
T2w = T_inv(Tw2)
T21 = np.matmul(T2w, Tw1)
#rospy.sleep(10)
#This is object1 in second pose
p_o2_prime = PoseStamped(header = Header(frame_id="test"), #robot.get_planning_frame()
pose=Pose(position=Point(0.7,-0.9,0.7),
orientation=Quaternion(0.3826834,0,0,-0.9238795)))
#scene.add_box("object1", p_o2_prime, (0.1, 0.1, 0.5))
Tw2_prime = PoseStamped_2_mat(p_o2_prime)
Tw1_prime = np.matmul(Tw2_prime, T21)
#rospy.sleep(2)
print "============ Generating plan 2"
#This is object2 in second pose
p_o1_prime = Mat_2_posestamped(Tw1_prime, f_id="test") # robot.get_planning_frame()
#scene.add_box("object2", p_o1_prime, (0.1, 0.1, 0.2))