分而治之解决一个数的幂,运行时分析与主定理
Divide and Conquer to solve the power of a number, runtime analysis with master theorem
我实现了一个分治算法来计算一个数的幂:
public static void main(String[] args) {
System.out.println("Result: " + pow(2, 1));
System.out.println("Result: " + pow(2, 9));
System.out.println("Result: " + pow(2, 8));
System.out.println("Result: " + pow(2, 0));
}
private static int pow(int n, int pow) {
if(pow == 0) {
return 1;
}
if(pow > 2) {
int leftPow;
int rightPow;
if(pow % 2 != 0) {
leftPow = pow/2;
rightPow = pow/2+1;
} else {
leftPow = pow/2;
rightPow = leftPow;
}
return pow(n, leftPow) * pow(n, rightPow);
} else {
if(pow == 1) {
return n;
} else {
return n * n;
}
}
}
我的方法似乎有效,因为输出是:
Result: 2
Result: 512
Result: 256
Result: 1
现在我正在尝试使用 Master-Theorem:
来确定我的算法的运行时间
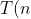&space;=&space;a*T(n/b)+f(n))
我假设
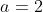 ,由于递归调用出现了两次,
,由于递归调用出现了两次,
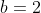 ,因为我要从一个问题中创建两个子问题
,因为我要从一个问题中创建两个子问题
和&space;=&space;1) ,因为组合结果需要常数时间。
,因为组合结果需要常数时间。
分水岭常数(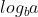 )应该是
)应该是 .
.
根据这些值,我假设定理的第一条规则成立:
&space;=&space;O(n%5E%7B%5Calpha-%5Cvarepsilon&space;%7D)) ,
,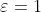 ,因为
,因为 &space;=&space;O(n%5E%7B1-1%7D)&space;=&space;1) 。
。
因此运行时间应该是:
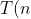=%5CTheta&space;(n%5E%7B%5Calpha%7D)&space;=&space;%5CTheta&space;(n)) .
.
我对这个结果很不确定,因为我从来没有遇到过这种情况&space;=&space;1) 。
。
我的分析是否正确?
首先,您应该注意到复杂性将根据 pow 进行解释。因此,n 在您的分析中意味着 pow 而不是您程序中的 n 变量。
其次,由于比较和乘法运算的次数是常数(你的程序小于10),所以f(n) = \Theta(1)这里可以写成f(n) = 1。
所以复杂度是T(n) = 2T(n/2) + 1(你也可以看Akra-Bazzi方法),T(n) = \Theta(n).
我实现了一个分治算法来计算一个数的幂:
public static void main(String[] args) {
System.out.println("Result: " + pow(2, 1));
System.out.println("Result: " + pow(2, 9));
System.out.println("Result: " + pow(2, 8));
System.out.println("Result: " + pow(2, 0));
}
private static int pow(int n, int pow) {
if(pow == 0) {
return 1;
}
if(pow > 2) {
int leftPow;
int rightPow;
if(pow % 2 != 0) {
leftPow = pow/2;
rightPow = pow/2+1;
} else {
leftPow = pow/2;
rightPow = leftPow;
}
return pow(n, leftPow) * pow(n, rightPow);
} else {
if(pow == 1) {
return n;
} else {
return n * n;
}
}
}
我的方法似乎有效,因为输出是:
Result: 2
Result: 512
Result: 256
Result: 1
现在我正在尝试使用 Master-Theorem:
来确定我的算法的运行时间我假设
,由于递归调用出现了两次,
,因为我要从一个问题中创建两个子问题
和,因为组合结果需要常数时间。
分水岭常数()应该是
.
根据这些值,我假设定理的第一条规则成立:
,
,因为
。
因此运行时间应该是:
.
我对这个结果很不确定,因为我从来没有遇到过这种情况。
我的分析是否正确?
首先,您应该注意到复杂性将根据 pow 进行解释。因此,n 在您的分析中意味着 pow 而不是您程序中的 n 变量。
其次,由于比较和乘法运算的次数是常数(你的程序小于10),所以f(n) = \Theta(1)这里可以写成f(n) = 1。
所以复杂度是T(n) = 2T(n/2) + 1(你也可以看Akra-Bazzi方法),T(n) = \Theta(n).