传递大量时间相关数据来求解 python 中的微分方程,
Passing large time dependent data to solve differential equation in python,
考虑这个简单的first-order微分方程:
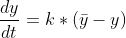
其中k是一个常数,值为0.5,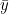 是一个随时间变化的变量。
是一个随时间变化的变量。
我使用以下代码在不同时间输入 y_bar 的值,效果很好。
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
def get_y_bar(t):
if t>=0 and t<=1:
return 0.0
elif t<=2:
return 1.0
elif t<=3:
return 2.0
elif t<=4:
return 3.0
elif t<=5:
return 4.0
else:
return 5.0
def ode(y,t):
k=0.5
y_bar=get_y_bar(t)
dy=k*(y_bar-y)
return dy
y0=0.0
t0=np.linspace(0,10,100)
sol=odeint(ode,y0,t0)
plt.plot(t0,sol)
plt.show()
但是,这种方法只有当我的数据量很小,可以手动使用if..elif..else循环输入时才可行。如果我在较小的时间步长中有较大的 y_bar 值(例如,t= 0.01、0.025、0.03、...、5.0),我该怎么办??
我有 CSV 格式的数据并尝试遍历数据但卡住了!!有什么简单的方法可以做到这一点??
def get_y_bar(t):
data=np.genfromtxt('data.csv',delimiter=',')
time=data[:,0]
y_bar=data[:,1]
for i in range(len(time)):
if t>=time[i] and t<=time[i=1]:
return y_bar[i]
else:
我不确定我是否完全理解你的问题。但是如果你想替换 get_y_bar 中的无数 elif 循环,试试这个:
import math
def get_y_bar(t):
return math.floor(t)
即math.floor(4.2)会return4,也就是小于4.2
的最大整数
使用这种方法,您将在每次 odeint 调用您的 ode 函数时加载您的文件,这将是非常低效的。
解决问题的更方便的方法是使用 scipy.interpolate.interp1d 替换 get_y_bar 函数,改为 kind = zero,即 常数插值 .您应该在 ode 函数之外执行此插值,因此您只执行一次。
考虑这个简单的first-order微分方程:
其中k是一个常数,值为0.5,是一个随时间变化的变量。
我使用以下代码在不同时间输入 y_bar 的值,效果很好。
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
def get_y_bar(t):
if t>=0 and t<=1:
return 0.0
elif t<=2:
return 1.0
elif t<=3:
return 2.0
elif t<=4:
return 3.0
elif t<=5:
return 4.0
else:
return 5.0
def ode(y,t):
k=0.5
y_bar=get_y_bar(t)
dy=k*(y_bar-y)
return dy
y0=0.0
t0=np.linspace(0,10,100)
sol=odeint(ode,y0,t0)
plt.plot(t0,sol)
plt.show()
但是,这种方法只有当我的数据量很小,可以手动使用if..elif..else循环输入时才可行。如果我在较小的时间步长中有较大的 y_bar 值(例如,t= 0.01、0.025、0.03、...、5.0),我该怎么办??
我有 CSV 格式的数据并尝试遍历数据但卡住了!!有什么简单的方法可以做到这一点??
def get_y_bar(t):
data=np.genfromtxt('data.csv',delimiter=',')
time=data[:,0]
y_bar=data[:,1]
for i in range(len(time)):
if t>=time[i] and t<=time[i=1]:
return y_bar[i]
else:
我不确定我是否完全理解你的问题。但是如果你想替换 get_y_bar 中的无数 elif 循环,试试这个:
import math
def get_y_bar(t):
return math.floor(t)
即math.floor(4.2)会return4,也就是小于4.2
使用这种方法,您将在每次 odeint 调用您的 ode 函数时加载您的文件,这将是非常低效的。
解决问题的更方便的方法是使用 scipy.interpolate.interp1d 替换 get_y_bar 函数,改为 kind = zero,即 常数插值 .您应该在 ode 函数之外执行此插值,因此您只执行一次。