如何在 Matlab 中求解矩阵?
How to solve for matrix in Matlab?
如何求解 ,其中
,其中 和
和 和
和
) 在最小二乘意义上 在 matlab 中?
在最小二乘意义上 在 matlab 中?
所以我想将最小化 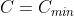 作为输出。
作为输出。
重写数量以最小化为
||Xa - b||^2
=(Frobenius范数的定义)
Tr{(Xa - b) (Xa - b)'}
=(展开矩阵乘积表达式)
Tr{Xaa'X' - ba'X' - Xab' + bb'}
=(迹算子的线性度)
Tr{Xaa'X'} - Tr{ba'X'} - Tr{Xab'} + Tr{bb'}
=(矩阵转置的迹 = 矩阵的迹)
Tr{Xaa'X'} - 2 Tr{ba'X'} + Tr{bb'}
其中'表示转置算子(因为涉及的所有矩阵都是实数,所以转置和共轭转置是一样的)。
现在,如果您参考 Matrix Cookbook 的第 2.5 节,您会发现
Tr{Xaa'X'}的导数是2Xaa'(见等式111),Tr{ba'X'}的导数是ba'(见等式104),Tr{bb'}的导数是0(因为这个表达式不依赖于X)。
(对矩阵X进行微分)。
因此,最小化兴趣量的矩阵满足
2Xaa' = 2ba'
Xaa' = ba'
因此,您可以使用 MATLAB 的矩阵右除运算符 / 来计算 X:
X = b * a' / (a * a');
如何求解,其中
和
和
在最小二乘意义上 在 matlab 中?
所以我想将最小化 作为输出。
重写数量以最小化为
||Xa - b||^2
=(Frobenius范数的定义)
Tr{(Xa - b) (Xa - b)'}
=(展开矩阵乘积表达式)
Tr{Xaa'X' - ba'X' - Xab' + bb'}
=(迹算子的线性度)
Tr{Xaa'X'} - Tr{ba'X'} - Tr{Xab'} + Tr{bb'}
=(矩阵转置的迹 = 矩阵的迹)
Tr{Xaa'X'} - 2 Tr{ba'X'} + Tr{bb'}
其中'表示转置算子(因为涉及的所有矩阵都是实数,所以转置和共轭转置是一样的)。
现在,如果您参考 Matrix Cookbook 的第 2.5 节,您会发现
Tr{Xaa'X'}的导数是2Xaa'(见等式111),Tr{ba'X'}的导数是ba'(见等式104),Tr{bb'}的导数是0(因为这个表达式不依赖于X)。
(对矩阵X进行微分)。
因此,最小化兴趣量的矩阵满足
2Xaa' = 2ba'
Xaa' = ba'
因此,您可以使用 MATLAB 的矩阵右除运算符 / 来计算 X:
X = b * a' / (a * a');