一个图可能有多个最小生成树
It is possible for a graph to have multiple minimum spanning trees
令G=(V, E) 为无向图，其所有边都具有唯一权重。是真的吗
G 有一个唯一的 MST？或者G也可以有多个MST？
根据 MST 的定义（来源：wikipedia）-
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.
目标是覆盖 所有 个顶点，同时具有 最低 边权重和。此外，生成树 (ST) 是 tree，因此没有循环 -
在上图中，橘子树是ST，但是，只有最上面的树可以是MST（边权和为7）。
编辑
反证法:
设 
be an undirected graph with unique edge weights. Let 
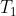and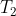 
为图形的两个 distinct 最小生成树。
让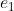
be the edge with lowest weight present in 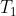, but, not in 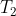. Similarly, let 
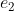be the edge in 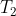, but, not in .
现在，由于边权重是唯一的，不失一般性，令
.
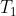此外，如果我们添加 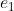in 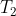, a cycle will form with 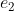. To remove the cycle, let us remove the edge 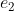from 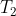. Thus, we have a Spanning Tree 
。
这个ST，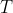
, now has total weight less than 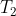; but, this is a contradiction, since, 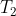已经是MST了。
因此，我们假设 有两个 MST 是错误的。证明到此结束。
令G=(V, E) 为无向图，其所有边都具有唯一权重。是真的吗 G 有一个唯一的 MST？或者G也可以有多个MST？
根据 MST 的定义（来源：wikipedia）-
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight.
目标是覆盖 所有 个顶点，同时具有 最低 边权重和。此外，生成树 (ST) 是 tree，因此没有循环 -
在上图中，橘子树是ST，但是，只有最上面的树可以是MST（边权和为7）。
编辑
反证法:
设 be an undirected graph with unique edge weights. Let
and
为图形的两个 distinct 最小生成树。
让 be the edge with lowest weight present in
, but, not in
. Similarly, let
be the edge in
, but, not in
.
现在，由于边权重是唯一的，不失一般性，令.
此外，如果我们添加 in
, a cycle will form with
. To remove the cycle, let us remove the edge
from
. Thus, we have a Spanning Tree
。
这个ST，, now has total weight less than
; but, this is a contradiction, since,
已经是MST了。
因此，我们假设 有两个 MST 是错误的。证明到此结束。