当输入接近于 0 时 Newton-Raphson 除法算法的初始值
Initial value for Newton-Raphson Division algorithm when input is close to 0
我正在通过 FPGA 在 S15.16 中对来自 [-16:16] 的值实施 Newton-Raphson 除法 算法。对于来自 |[1:16]| 的值,我通过 3 次迭代实现了 10e-9 的 MSE。我初始化值 a0 的方法是对每个范围内的中间点取反:
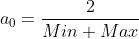
一些例子是:
- 从范围 1 <= x < 2: a0 = 2/3
- 从范围 6 <= x < 7: a0 = 2/13
- 从范围 15 <= x < 16: a0 = 2/31
这个近似值效果很好,如下图所示:
所以,这里的问题是在[0:1]所包含的范围内。如何找到最佳初始值或初始值的近似值?
在维基百科中说:
对于选择初始估计值 X0 的子问题,可以方便地将 bit-shift 应用于除数 D 以对其进行缩放,以便 0.5 ≤ D ≤ 1;通过对分子 N 应用相同的 bit-shift,可以确保商不会改变。然后可以使用
形式的线性近似
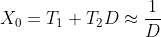
初始化Newton-Raphson。为了最小化区间 [0.5,1] 上此近似误差的绝对值的最大值,应使用
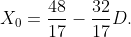
好的,这个近似值适用于范围 [0.5:1],但是:
- 当值趋于变小,接近 0 时会发生什么。例如:
0.1、0.01、0.001、0.00001...等等?我在这里看到一个问题,因为我认为
[0.001:0.01]、[0.01:0.1]... 等 之间的每个范围都需要一个初始值
- 对于较小的值,最好应用其他算法,例如 Goldschmidt 除法算法?
这些是我为模拟定点中的 Newton-Raphson 除法 而实现的代码:
i = 0
# 16 fractional bits
SHIFT = 2 ** 16
# Lut with "optimal?" values to init NRD algorithm
LUT = np.round(1 / np.arange(0.5, 16, 1) * SHIFT).astype(np.int64)
LUT_f = 1 / np.arange(0.5, 16, 1)
# Function to simulates the NRD algorithm in S15.16 over a FPGA
def FIXED_RECIPROCAL(x):
# Smart adressing to the initial iteration value
adress = x >> 16
# Get the value from LUT
a0 = LUT[adress]
# Algorithm with only 3 iterations
for i in range(3):
s1 = (a0*a0) >> 16
s2 = (x*s1) >> 16
a0 = (a0 << 1) - s2
# Return rescaled value (Only for analysis purposes)
return(a0 / SHIFT)
# ----- TEST ----- #
t = np.arange(1, 16, 0.1)
teor = 1 / t
t_fixed = (t * SHIFT).astype(np.int32)
prac = np.zeros(len(t))
for value in t_fixed:
prac[i] = FIXED_RECIPROCAL(value)
i = i + 1
# Get and print Errors
errors = abs(prac - teor)
mse = ((prac - teor)**2).mean(axis=None)
print("Max Error : %s" % ('{:.3E}'.format(np.max(errors))))
print("MSE: : %s" % ('{:.3E}'.format(mse)))
# Print the obtained values:
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.plot(t, teor, label='Theorical division')
plt.plot(t, prac, '.', label='Newton-Raphson Division')
plt.legend(fontsize=16)
plt.title('Float 32 theorical division Vs. S15.16 Newton-Raphson division', fontsize=22)
plt.xlabel('x', fontsize=20)
plt.ylabel('1 / x', fontsize=20)
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
下面的 ISO-C99 代码演示了如何实现基于 Newton-Raphson 的 s15.16 除法的几乎正确的舍入实现,使用 2 kb 查找 table 进行初始倒数近似,并使用一个数字32x32 位乘法器能够提供完整乘积的低 32 位和高 32 位。为了便于实施,有符号的 s15.16 除法被映射回无符号的 16.16 除法,用于 [0, 231].
中的操作数
我们需要通过保持操作数规范化来充分利用 32 位数据路径。本质上,我们正在将计算转换为准浮点格式。这需要优先级编码器在初始归一化步骤中找到被除数和除数中的最高有效位。为了软件方便,这被映射到 CLZ(计数前导零)操作,存在于许多处理器中,在下面的代码中。
计算除数的倒数 b 后,我们乘以被除数 a 以确定原始商数 q = (1/b)*a。为了正确地四舍五入到最接近或均匀,我们需要计算商 a 的余数及其增量和减量。正确舍入的商对应于具有最小余数的候选商。
为了使其完美运行,我们需要一个与数学结果相差 1 ulp 以内的原始商。不幸的是,不是这里的情况,因为原始商偶尔会偏离 ±2 ulp。我们在一些中间计算中需要有效的 33 位,这可以在软件中模拟,但我现在没有时间来解决这个问题。代码“按原样”在超过 99.999% 的随机测试用例中提供正确舍入的结果。
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define TAB_BITS_IN (8) /* 256 entry LUT */
#define TAB_BITS_OUT (9) /* 9 bits effective, 8 bits stored */
#define TRUNC_COMP (1) /* compensate truncation in fixed-point multiply */
int clz (uint32_t a); // count leadzing zeros: a priority encoder
uint32_t umul32_hi (uint32_t a, uint32_t b); // upper half of 32x32-bit product
/* i in [0,255]: (int)(1.0 / (1.0 + 1.0/512.0 + i / 256.0) * 512 + .5) & 0xff
In a second step tuned to minimize the number of incorrect results with the
specific implementation of the two refinement steps chosen.
*/
static uint8_t rcp_tab[256] =
{
0xff, 0xfd, 0xfb, 0xf9, 0xf7, 0xf5, 0xf3, 0xf1,
0xf0, 0xee, 0xec, 0xea, 0xe8, 0xe6, 0xe5, 0xe3,
0xe1, 0xdf, 0xdd, 0xdc, 0xda, 0xd8, 0xd7, 0xd5,
0xd3, 0xd2, 0xd0, 0xce, 0xcd, 0xcb, 0xc9, 0xc8,
0xc6, 0xc5, 0xc3, 0xc2, 0xc0, 0xbf, 0xbd, 0xbc,
0xba, 0xb9, 0xb7, 0xb6, 0xb4, 0xb3, 0xb1, 0xb0,
0xae, 0xad, 0xac, 0xaa, 0xa9, 0xa7, 0xa6, 0xa5,
0xa4, 0xa2, 0xa1, 0x9f, 0x9e, 0x9d, 0x9c, 0x9a,
0x99, 0x98, 0x96, 0x95, 0x94, 0x93, 0x91, 0x90,
0x8f, 0x8e, 0x8c, 0x8b, 0x8a, 0x89, 0x88, 0x87,
0x86, 0x84, 0x83, 0x82, 0x81, 0x80, 0x7f, 0x7e,
0x7c, 0x7b, 0x7a, 0x79, 0x78, 0x77, 0x76, 0x74,
0x74, 0x73, 0x71, 0x71, 0x70, 0x6f, 0x6e, 0x6d,
0x6b, 0x6b, 0x6a, 0x68, 0x67, 0x67, 0x66, 0x65,
0x64, 0x63, 0x62, 0x61, 0x60, 0x5f, 0x5e, 0x5d,
0x5c, 0x5b, 0x5b, 0x59, 0x58, 0x58, 0x56, 0x56,
0x55, 0x54, 0x53, 0x52, 0x51, 0x51, 0x50, 0x4f,
0x4e, 0x4e, 0x4c, 0x4b, 0x4b, 0x4a, 0x48, 0x48,
0x48, 0x46, 0x46, 0x45, 0x44, 0x43, 0x43, 0x42,
0x41, 0x40, 0x3f, 0x3f, 0x3e, 0x3d, 0x3c, 0x3b,
0x3b, 0x3a, 0x39, 0x38, 0x38, 0x37, 0x36, 0x36,
0x35, 0x34, 0x34, 0x33, 0x32, 0x31, 0x30, 0x30,
0x2f, 0x2e, 0x2e, 0x2d, 0x2d, 0x2c, 0x2b, 0x2a,
0x2a, 0x29, 0x28, 0x27, 0x27, 0x26, 0x26, 0x25,
0x24, 0x23, 0x23, 0x22, 0x21, 0x21, 0x21, 0x20,
0x1f, 0x1f, 0x1e, 0x1d, 0x1d, 0x1c, 0x1c, 0x1b,
0x1a, 0x19, 0x19, 0x19, 0x18, 0x17, 0x17, 0x16,
0x16, 0x15, 0x14, 0x13, 0x13, 0x12, 0x12, 0x11,
0x11, 0x10, 0x0f, 0x0f, 0x0e, 0x0e, 0x0e, 0x0d,
0x0c, 0x0c, 0x0b, 0x0b, 0x0a, 0x0a, 0x09, 0x08,
0x08, 0x07, 0x07, 0x07, 0x06, 0x05, 0x05, 0x04,
0x04, 0x03, 0x03, 0x02, 0x02, 0x01, 0x01, 0x01
};
/* Divide two u16.16 fixed-point operands each in [0, 2**31]. Attempt to round
the result to nearest of even. Currently this does not always succeed. We
would need effectively 33 bits in intermediate computation for that, so the
raw quotient is within +/- 1 ulp of the mathematical result.
*/
uint32_t div_core (uint32_t a, uint32_t b)
{
/* normalize dividend and divisor to [1,2); bit 31 is the integer bit */
uint8_t lza = clz (a);
uint8_t lzb = clz (b);
uint32_t na = a << lza;
uint32_t nb = b << lzb;
/* LUT is addressed by most significant fraction bits of divisor */
uint32_t idx = (nb >> (32 - 1 - TAB_BITS_IN)) & 0xff;
uint32_t rcp = rcp_tab [idx] | 0x100; // add implicit msb
/* first NR iteration */
uint32_t f = (rcp * rcp) << (32 - 2*TAB_BITS_OUT);
uint32_t p = umul32_hi (f, nb);
rcp = (rcp << (32 - TAB_BITS_OUT)) - p;
/* second NR iteration */
rcp = rcp << 1;
p = umul32_hi (rcp, nb);
rcp = umul32_hi (rcp, 0 - p);
/* compute raw quotient as (1/b)*a; off by at most +/- 2ulps */
rcp = (rcp << 1) | TRUNC_COMP;
uint32_t quot = umul32_hi (rcp, na);
uint8_t shift = lza - lzb + 15;
quot = (shift > 31) ? 0 : (quot >> shift);
/* round quotient using 4:1 mux */
uint32_t ah = a << 16;
uint32_t prod = quot * b;
uint32_t rem1 = abs (ah - prod);
uint32_t rem2 = abs (ah - prod - b);
uint32_t rem3 = abs (ah - prod + b);
int sel = (((rem2 < rem1) << 1) | ((rem3 < rem1) & (quot != 0)));
switch (sel) {
case 0:
default:
quot = quot;
break;
case 1:
quot = quot - 1;
break;
case 2: /* fall through */
case 3:
quot = quot + 1;
break;
}
return quot;
}
int32_t div_s15p16 (int32_t a, int32_t b)
{
uint32_t aa = abs (a);
uint32_t ab = abs (b);
uint32_t quot = div_core (aa, ab);
quot = ((a ^ b) & 0x80000000) ? (0 - quot) : quot;
return (int32_t)quot;
}
uint64_t umul32_wide (uint32_t a, uint32_t b)
{
return ((uint64_t)a) * b;
}
uint32_t umul32_hi (uint32_t a, uint32_t b)
{
return (uint32_t)(umul32_wide (a, b) >> 32);
}
#define VARIANT (1)
int clz (uint32_t a)
{
#if VARIANT == 1
static const uint8_t clz_tab[32] = {
31, 22, 30, 21, 18, 10, 29, 2, 20, 17, 15, 13, 9, 6, 28, 1,
23, 19, 11, 3, 16, 14, 7, 24, 12, 4, 8, 25, 5, 26, 27, 0
};
a |= a >> 16;
a |= a >> 8;
a |= a >> 4;
a |= a >> 2;
a |= a >> 1;
return clz_tab [0x07c4acddu * a >> 27] + (!a);
#elif VARIANT == 2
uint32_t b;
int n = 31 + (!a);
if ((b = (a & 0xffff0000u))) { n -= 16; a = b; }
if ((b = (a & 0xff00ff00u))) { n -= 8; a = b; }
if ((b = (a & 0xf0f0f0f0u))) { n -= 4; a = b; }
if ((b = (a & 0xccccccccu))) { n -= 2; a = b; }
if (( (a & 0xaaaaaaaau))) { n -= 1; }
return n;
#elif VARIANT == 3
int n = 0;
if (!(a & 0xffff0000u)) { n |= 16; a <<= 16; }
if (!(a & 0xff000000u)) { n |= 8; a <<= 8; }
if (!(a & 0xf0000000u)) { n |= 4; a <<= 4; }
if (!(a & 0xc0000000u)) { n |= 2; a <<= 2; }
if ((int32_t)a >= 0) n++;
if ((int32_t)a == 0) n++;
return n;
#elif VARIANT == 4
uint32_t b;
int n = 32;
if ((b = (a >> 16))) { n = n - 16; a = b; }
if ((b = (a >> 8))) { n = n - 8; a = b; }
if ((b = (a >> 4))) { n = n - 4; a = b; }
if ((b = (a >> 2))) { n = n - 2; a = b; }
if ((b = (a >> 1))) return n - 2;
return n - a;
#endif
}
uint32_t div_core_ref (uint32_t a, uint32_t b)
{
int64_t quot = ((int64_t)a << 16) / b;
/* round to nearest or even */
int64_t rem1 = ((int64_t)a << 16) - quot * b;
int64_t rem2 = rem1 - b;
if (llabs (rem2) < llabs (rem1)) quot++;
if ((llabs (rem2) == llabs (rem1)) && (quot & 1)) quot &= ~1;
return (uint32_t)quot;
}
// George Marsaglia's KISS PRNG, period 2**123. Newsgroup sci.math, 21 Jan 1999
// Bug fix: Greg Rose, "KISS: A Bit Too Simple" http://eprint.iacr.org/2011/007
static uint32_t kiss_z=362436069, kiss_w=521288629;
static uint32_t kiss_jsr=123456789, kiss_jcong=380116160;
#define znew (kiss_z=36969*(kiss_z&65535)+(kiss_z>>16))
#define wnew (kiss_w=18000*(kiss_w&65535)+(kiss_w>>16))
#define MWC ((znew<<16)+wnew )
#define SHR3 (kiss_jsr^=(kiss_jsr<<13),kiss_jsr^=(kiss_jsr>>17), \
kiss_jsr^=(kiss_jsr<<5))
#define CONG (kiss_jcong=69069*kiss_jcong+1234567)
#define KISS ((MWC^CONG)+SHR3)
int main (void)
{
uint64_t count = 0ULL, stats[3] = {0ULL, 0ULL, 0ULL};
uint32_t a, b, res, ref;
do {
/* random dividend and divisor, avoiding overflow and divison by zero */
do {
a = KISS % 0x80000001u;
b = KISS % 0x80000001u;
} while ((b == 0) || ((((uint64_t)a << 16) / b) > 0x80000000ULL));
/* compute function under test and reference result */
ref = div_core_ref (a, b);
res = div_core (a, b);
if (llabs ((int64_t)res - (int64_t)ref) > 1) {
printf ("\nerror: a=%08x b=%08x res=%08x ref=%08x\n", a, b, res, ref);
break;
} else {
stats[(int64_t)res - (int64_t)ref + 1]++;
}
count++;
if (!(count & 0xffffff)) {
printf ("\r[-1]=%llu [0]=%llu [+1]=%llu", stats[0], stats[1], stats[2]);
}
} while (count);
return EXIT_SUCCESS;
}
我正在通过 FPGA 在 S15.16 中对来自 [-16:16] 的值实施 Newton-Raphson 除法 算法。对于来自 |[1:16]| 的值,我通过 3 次迭代实现了 10e-9 的 MSE。我初始化值 a0 的方法是对每个范围内的中间点取反:
一些例子是:
- 从范围 1 <= x < 2: a0 = 2/3
- 从范围 6 <= x < 7: a0 = 2/13
- 从范围 15 <= x < 16: a0 = 2/31
这个近似值效果很好,如下图所示:
所以,这里的问题是在[0:1]所包含的范围内。如何找到最佳初始值或初始值的近似值?
在维基百科中说:
对于选择初始估计值 X0 的子问题,可以方便地将 bit-shift 应用于除数 D 以对其进行缩放,以便 0.5 ≤ D ≤ 1;通过对分子 N 应用相同的 bit-shift,可以确保商不会改变。然后可以使用
形式的线性近似初始化Newton-Raphson。为了最小化区间 [0.5,1] 上此近似误差的绝对值的最大值,应使用
好的,这个近似值适用于范围 [0.5:1],但是:
- 当值趋于变小,接近 0 时会发生什么。例如:
0.1、0.01、0.001、0.00001...等等?我在这里看到一个问题,因为我认为
[0.001:0.01]、[0.01:0.1]... 等 之间的每个范围都需要一个初始值
- 对于较小的值,最好应用其他算法,例如 Goldschmidt 除法算法?
这些是我为模拟定点中的 Newton-Raphson 除法 而实现的代码:
i = 0
# 16 fractional bits
SHIFT = 2 ** 16
# Lut with "optimal?" values to init NRD algorithm
LUT = np.round(1 / np.arange(0.5, 16, 1) * SHIFT).astype(np.int64)
LUT_f = 1 / np.arange(0.5, 16, 1)
# Function to simulates the NRD algorithm in S15.16 over a FPGA
def FIXED_RECIPROCAL(x):
# Smart adressing to the initial iteration value
adress = x >> 16
# Get the value from LUT
a0 = LUT[adress]
# Algorithm with only 3 iterations
for i in range(3):
s1 = (a0*a0) >> 16
s2 = (x*s1) >> 16
a0 = (a0 << 1) - s2
# Return rescaled value (Only for analysis purposes)
return(a0 / SHIFT)
# ----- TEST ----- #
t = np.arange(1, 16, 0.1)
teor = 1 / t
t_fixed = (t * SHIFT).astype(np.int32)
prac = np.zeros(len(t))
for value in t_fixed:
prac[i] = FIXED_RECIPROCAL(value)
i = i + 1
# Get and print Errors
errors = abs(prac - teor)
mse = ((prac - teor)**2).mean(axis=None)
print("Max Error : %s" % ('{:.3E}'.format(np.max(errors))))
print("MSE: : %s" % ('{:.3E}'.format(mse)))
# Print the obtained values:
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.plot(t, teor, label='Theorical division')
plt.plot(t, prac, '.', label='Newton-Raphson Division')
plt.legend(fontsize=16)
plt.title('Float 32 theorical division Vs. S15.16 Newton-Raphson division', fontsize=22)
plt.xlabel('x', fontsize=20)
plt.ylabel('1 / x', fontsize=20)
plt.xticks(fontsize=16)
plt.yticks(fontsize=16)
下面的 ISO-C99 代码演示了如何实现基于 Newton-Raphson 的 s15.16 除法的几乎正确的舍入实现,使用 2 kb 查找 table 进行初始倒数近似,并使用一个数字32x32 位乘法器能够提供完整乘积的低 32 位和高 32 位。为了便于实施,有符号的 s15.16 除法被映射回无符号的 16.16 除法,用于 [0, 231].
中的操作数我们需要通过保持操作数规范化来充分利用 32 位数据路径。本质上,我们正在将计算转换为准浮点格式。这需要优先级编码器在初始归一化步骤中找到被除数和除数中的最高有效位。为了软件方便,这被映射到 CLZ(计数前导零)操作,存在于许多处理器中,在下面的代码中。
计算除数的倒数 b 后,我们乘以被除数 a 以确定原始商数 q = (1/b)*a。为了正确地四舍五入到最接近或均匀,我们需要计算商 a 的余数及其增量和减量。正确舍入的商对应于具有最小余数的候选商。
为了使其完美运行,我们需要一个与数学结果相差 1 ulp 以内的原始商。不幸的是,不是这里的情况,因为原始商偶尔会偏离 ±2 ulp。我们在一些中间计算中需要有效的 33 位,这可以在软件中模拟,但我现在没有时间来解决这个问题。代码“按原样”在超过 99.999% 的随机测试用例中提供正确舍入的结果。
#include <stdio.h>
#include <stdlib.h>
#include <stdint.h>
#define TAB_BITS_IN (8) /* 256 entry LUT */
#define TAB_BITS_OUT (9) /* 9 bits effective, 8 bits stored */
#define TRUNC_COMP (1) /* compensate truncation in fixed-point multiply */
int clz (uint32_t a); // count leadzing zeros: a priority encoder
uint32_t umul32_hi (uint32_t a, uint32_t b); // upper half of 32x32-bit product
/* i in [0,255]: (int)(1.0 / (1.0 + 1.0/512.0 + i / 256.0) * 512 + .5) & 0xff
In a second step tuned to minimize the number of incorrect results with the
specific implementation of the two refinement steps chosen.
*/
static uint8_t rcp_tab[256] =
{
0xff, 0xfd, 0xfb, 0xf9, 0xf7, 0xf5, 0xf3, 0xf1,
0xf0, 0xee, 0xec, 0xea, 0xe8, 0xe6, 0xe5, 0xe3,
0xe1, 0xdf, 0xdd, 0xdc, 0xda, 0xd8, 0xd7, 0xd5,
0xd3, 0xd2, 0xd0, 0xce, 0xcd, 0xcb, 0xc9, 0xc8,
0xc6, 0xc5, 0xc3, 0xc2, 0xc0, 0xbf, 0xbd, 0xbc,
0xba, 0xb9, 0xb7, 0xb6, 0xb4, 0xb3, 0xb1, 0xb0,
0xae, 0xad, 0xac, 0xaa, 0xa9, 0xa7, 0xa6, 0xa5,
0xa4, 0xa2, 0xa1, 0x9f, 0x9e, 0x9d, 0x9c, 0x9a,
0x99, 0x98, 0x96, 0x95, 0x94, 0x93, 0x91, 0x90,
0x8f, 0x8e, 0x8c, 0x8b, 0x8a, 0x89, 0x88, 0x87,
0x86, 0x84, 0x83, 0x82, 0x81, 0x80, 0x7f, 0x7e,
0x7c, 0x7b, 0x7a, 0x79, 0x78, 0x77, 0x76, 0x74,
0x74, 0x73, 0x71, 0x71, 0x70, 0x6f, 0x6e, 0x6d,
0x6b, 0x6b, 0x6a, 0x68, 0x67, 0x67, 0x66, 0x65,
0x64, 0x63, 0x62, 0x61, 0x60, 0x5f, 0x5e, 0x5d,
0x5c, 0x5b, 0x5b, 0x59, 0x58, 0x58, 0x56, 0x56,
0x55, 0x54, 0x53, 0x52, 0x51, 0x51, 0x50, 0x4f,
0x4e, 0x4e, 0x4c, 0x4b, 0x4b, 0x4a, 0x48, 0x48,
0x48, 0x46, 0x46, 0x45, 0x44, 0x43, 0x43, 0x42,
0x41, 0x40, 0x3f, 0x3f, 0x3e, 0x3d, 0x3c, 0x3b,
0x3b, 0x3a, 0x39, 0x38, 0x38, 0x37, 0x36, 0x36,
0x35, 0x34, 0x34, 0x33, 0x32, 0x31, 0x30, 0x30,
0x2f, 0x2e, 0x2e, 0x2d, 0x2d, 0x2c, 0x2b, 0x2a,
0x2a, 0x29, 0x28, 0x27, 0x27, 0x26, 0x26, 0x25,
0x24, 0x23, 0x23, 0x22, 0x21, 0x21, 0x21, 0x20,
0x1f, 0x1f, 0x1e, 0x1d, 0x1d, 0x1c, 0x1c, 0x1b,
0x1a, 0x19, 0x19, 0x19, 0x18, 0x17, 0x17, 0x16,
0x16, 0x15, 0x14, 0x13, 0x13, 0x12, 0x12, 0x11,
0x11, 0x10, 0x0f, 0x0f, 0x0e, 0x0e, 0x0e, 0x0d,
0x0c, 0x0c, 0x0b, 0x0b, 0x0a, 0x0a, 0x09, 0x08,
0x08, 0x07, 0x07, 0x07, 0x06, 0x05, 0x05, 0x04,
0x04, 0x03, 0x03, 0x02, 0x02, 0x01, 0x01, 0x01
};
/* Divide two u16.16 fixed-point operands each in [0, 2**31]. Attempt to round
the result to nearest of even. Currently this does not always succeed. We
would need effectively 33 bits in intermediate computation for that, so the
raw quotient is within +/- 1 ulp of the mathematical result.
*/
uint32_t div_core (uint32_t a, uint32_t b)
{
/* normalize dividend and divisor to [1,2); bit 31 is the integer bit */
uint8_t lza = clz (a);
uint8_t lzb = clz (b);
uint32_t na = a << lza;
uint32_t nb = b << lzb;
/* LUT is addressed by most significant fraction bits of divisor */
uint32_t idx = (nb >> (32 - 1 - TAB_BITS_IN)) & 0xff;
uint32_t rcp = rcp_tab [idx] | 0x100; // add implicit msb
/* first NR iteration */
uint32_t f = (rcp * rcp) << (32 - 2*TAB_BITS_OUT);
uint32_t p = umul32_hi (f, nb);
rcp = (rcp << (32 - TAB_BITS_OUT)) - p;
/* second NR iteration */
rcp = rcp << 1;
p = umul32_hi (rcp, nb);
rcp = umul32_hi (rcp, 0 - p);
/* compute raw quotient as (1/b)*a; off by at most +/- 2ulps */
rcp = (rcp << 1) | TRUNC_COMP;
uint32_t quot = umul32_hi (rcp, na);
uint8_t shift = lza - lzb + 15;
quot = (shift > 31) ? 0 : (quot >> shift);
/* round quotient using 4:1 mux */
uint32_t ah = a << 16;
uint32_t prod = quot * b;
uint32_t rem1 = abs (ah - prod);
uint32_t rem2 = abs (ah - prod - b);
uint32_t rem3 = abs (ah - prod + b);
int sel = (((rem2 < rem1) << 1) | ((rem3 < rem1) & (quot != 0)));
switch (sel) {
case 0:
default:
quot = quot;
break;
case 1:
quot = quot - 1;
break;
case 2: /* fall through */
case 3:
quot = quot + 1;
break;
}
return quot;
}
int32_t div_s15p16 (int32_t a, int32_t b)
{
uint32_t aa = abs (a);
uint32_t ab = abs (b);
uint32_t quot = div_core (aa, ab);
quot = ((a ^ b) & 0x80000000) ? (0 - quot) : quot;
return (int32_t)quot;
}
uint64_t umul32_wide (uint32_t a, uint32_t b)
{
return ((uint64_t)a) * b;
}
uint32_t umul32_hi (uint32_t a, uint32_t b)
{
return (uint32_t)(umul32_wide (a, b) >> 32);
}
#define VARIANT (1)
int clz (uint32_t a)
{
#if VARIANT == 1
static const uint8_t clz_tab[32] = {
31, 22, 30, 21, 18, 10, 29, 2, 20, 17, 15, 13, 9, 6, 28, 1,
23, 19, 11, 3, 16, 14, 7, 24, 12, 4, 8, 25, 5, 26, 27, 0
};
a |= a >> 16;
a |= a >> 8;
a |= a >> 4;
a |= a >> 2;
a |= a >> 1;
return clz_tab [0x07c4acddu * a >> 27] + (!a);
#elif VARIANT == 2
uint32_t b;
int n = 31 + (!a);
if ((b = (a & 0xffff0000u))) { n -= 16; a = b; }
if ((b = (a & 0xff00ff00u))) { n -= 8; a = b; }
if ((b = (a & 0xf0f0f0f0u))) { n -= 4; a = b; }
if ((b = (a & 0xccccccccu))) { n -= 2; a = b; }
if (( (a & 0xaaaaaaaau))) { n -= 1; }
return n;
#elif VARIANT == 3
int n = 0;
if (!(a & 0xffff0000u)) { n |= 16; a <<= 16; }
if (!(a & 0xff000000u)) { n |= 8; a <<= 8; }
if (!(a & 0xf0000000u)) { n |= 4; a <<= 4; }
if (!(a & 0xc0000000u)) { n |= 2; a <<= 2; }
if ((int32_t)a >= 0) n++;
if ((int32_t)a == 0) n++;
return n;
#elif VARIANT == 4
uint32_t b;
int n = 32;
if ((b = (a >> 16))) { n = n - 16; a = b; }
if ((b = (a >> 8))) { n = n - 8; a = b; }
if ((b = (a >> 4))) { n = n - 4; a = b; }
if ((b = (a >> 2))) { n = n - 2; a = b; }
if ((b = (a >> 1))) return n - 2;
return n - a;
#endif
}
uint32_t div_core_ref (uint32_t a, uint32_t b)
{
int64_t quot = ((int64_t)a << 16) / b;
/* round to nearest or even */
int64_t rem1 = ((int64_t)a << 16) - quot * b;
int64_t rem2 = rem1 - b;
if (llabs (rem2) < llabs (rem1)) quot++;
if ((llabs (rem2) == llabs (rem1)) && (quot & 1)) quot &= ~1;
return (uint32_t)quot;
}
// George Marsaglia's KISS PRNG, period 2**123. Newsgroup sci.math, 21 Jan 1999
// Bug fix: Greg Rose, "KISS: A Bit Too Simple" http://eprint.iacr.org/2011/007
static uint32_t kiss_z=362436069, kiss_w=521288629;
static uint32_t kiss_jsr=123456789, kiss_jcong=380116160;
#define znew (kiss_z=36969*(kiss_z&65535)+(kiss_z>>16))
#define wnew (kiss_w=18000*(kiss_w&65535)+(kiss_w>>16))
#define MWC ((znew<<16)+wnew )
#define SHR3 (kiss_jsr^=(kiss_jsr<<13),kiss_jsr^=(kiss_jsr>>17), \
kiss_jsr^=(kiss_jsr<<5))
#define CONG (kiss_jcong=69069*kiss_jcong+1234567)
#define KISS ((MWC^CONG)+SHR3)
int main (void)
{
uint64_t count = 0ULL, stats[3] = {0ULL, 0ULL, 0ULL};
uint32_t a, b, res, ref;
do {
/* random dividend and divisor, avoiding overflow and divison by zero */
do {
a = KISS % 0x80000001u;
b = KISS % 0x80000001u;
} while ((b == 0) || ((((uint64_t)a << 16) / b) > 0x80000000ULL));
/* compute function under test and reference result */
ref = div_core_ref (a, b);
res = div_core (a, b);
if (llabs ((int64_t)res - (int64_t)ref) > 1) {
printf ("\nerror: a=%08x b=%08x res=%08x ref=%08x\n", a, b, res, ref);
break;
} else {
stats[(int64_t)res - (int64_t)ref + 1]++;
}
count++;
if (!(count & 0xffffff)) {
printf ("\r[-1]=%llu [0]=%llu [+1]=%llu", stats[0], stats[1], stats[2]);
}
} while (count);
return EXIT_SUCCESS;
}