使用 cvxr 在 objective 函数中将两个变量相乘
Multiply two variables in an objective function using cvxr
我想最小化下面的objective函数

有一些限制

另一位用户(我认为是 G. Grothendieck)建议使用 R 的 CVXR 包。
所以我按照 A Gentle Introduction to CVXR 上的说明制作我的代码
library(CVXR) # if necessary
x <- Variable(1)
y <- Variable(1)
objective <- Minimize(5*x^2 + 14*x*y + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, y >= 0, x + 2*y <=10, x + y<=6)
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF) # and here the error occured
## Error in construct_intermediate_chain(object, candidate_solvers, gp = gp): Problem does not follow DCP rules.
上如何将二次规划转化为线性规划?
我发现 McCormick envelopes 的提示有助于解决双线性公式部分  的问题。特别是
的问题。特别是 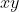 部分。
部分。
在 josliber 的答案末尾,他评论说,所有变量都应该有一个界限。在我的约束中没有上限,因此我插入了一个上限。这是一个任意的选择。如果解决方案在边界上,则必须使用新边界重新计算...
library(CVXR) # if necessary
x <- Variable(1)
y <- Variable(1)
w <- Variable(1)
objective <- Minimize(5*x^2 + 14*w + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, x <= 100,
y >= 0, y <= 100,
x+2*y <= 10,
x+y <= 6,
w >= 0, w >= 100*x + 100*y - 10000, # constraints according to McCormick envelopes
w <= 100*y, w <= 100*x) # constraints according to McCormick envelopes
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF)
solution_OF$value
## -125.0667
solution_OF$getValue(x)
## 2.933333
solution_OF$getValue(y)
## 3.066667
solution_OF$getValue(w)
## 1.000135e-30
这里的解决方案不是我预期的...当我用 solve.QP() 解决相同的 objective 函数时,我得到 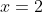 和
和 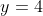 。要建立代码,请查看我的其他 question...
。要建立代码,请查看我的其他 question...
让我们检查一下代码:
# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108)
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)
# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b
# load the package and run solve.QP()
library(quadprog)
solve.QP(Dmat,dvec,Amat,bvec,meq=0,factorized=TRUE)
## $solution
## [1] 2 4 # these are the x and y results
##
## $value
## -587.9768
##
## and some more results...
问题:
- 为什么两个结果不同?
- 我在哪些解法中犯了错误?可以指出来吗?
- 当我从结果中输入 x 和 y 时,我没有得到
solve.QP() 替代项的 $value
- 做数学题时

- 如您所见,结果并不一致
- 我是不是搞错了?!
非常感谢!
问题在于
- 问题使用的是 factorized=TRUE
- 问题顶部的 objective 函数暗示 dvec[1] 与问题代码中显示的不同。
如果我们省略分解(默认为 FALSE)并始终使用问题中定义 Dmat、dvec、Amat 和 bvec 的代码,那么我们从 solve.QP 和手动计算 objective 基于解向量,均为-297。 ###### 之前的代码是从问题中逐字复制的。
# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108)
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)
# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b
######
library(quadprog)
ans <- solve.QP(Dmat,dvec,Amat,bvec)
str(ans)
## List of 6
## $ solution : num [1:2] 3 3
## $ value : num -297
## ...snip...
# manual calculation of objective function
t(ans$solution) %*% Dmat %*% ans$solution / 2 - dvec %*% ans$solution
## [,1]
## [1,] -297
# another manual calculation - coefficients come from Dmat and dvec
f <- function(x, y) (10 * x^2 + 2 * 14 * x * y + 20 * y^2) / 2 - (78 * x + 108 * y)
f(3, 3)
## [1] -297
我想最小化下面的objective函数
有一些限制
另一位用户(我认为是 G. Grothendieck)建议使用 R 的 CVXR 包。
所以我按照 A Gentle Introduction to CVXR 上的说明制作我的代码
library(CVXR) # if necessary
x <- Variable(1)
y <- Variable(1)
objective <- Minimize(5*x^2 + 14*x*y + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, y >= 0, x + 2*y <=10, x + y<=6)
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF) # and here the error occured
## Error in construct_intermediate_chain(object, candidate_solvers, gp = gp): Problem does not follow DCP rules.
上如何将二次规划转化为线性规划?
我发现 McCormick envelopes 的提示有助于解决双线性公式部分 的问题。特别是
部分。
在 josliber 的答案末尾,他评论说,所有变量都应该有一个界限。在我的约束中没有上限,因此我插入了一个上限。这是一个任意的选择。如果解决方案在边界上,则必须使用新边界重新计算...
library(CVXR) # if necessary
x <- Variable(1)
y <- Variable(1)
w <- Variable(1)
objective <- Minimize(5*x^2 + 14*w + 10*y^2 -76*x -108*y +292)
constraints <- list(x >= 0, x <= 100,
y >= 0, y <= 100,
x+2*y <= 10,
x+y <= 6,
w >= 0, w >= 100*x + 100*y - 10000, # constraints according to McCormick envelopes
w <= 100*y, w <= 100*x) # constraints according to McCormick envelopes
prob_OF <- Problem(objective, constraints)
solution_OF <- solve(prob_OF)
solution_OF$value
## -125.0667
solution_OF$getValue(x)
## 2.933333
solution_OF$getValue(y)
## 3.066667
solution_OF$getValue(w)
## 1.000135e-30
这里的解决方案不是我预期的...当我用 solve.QP() 解决相同的 objective 函数时,我得到 和
。要建立代码,请查看我的其他 question...
让我们检查一下代码:
# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108)
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)
# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b
# load the package and run solve.QP()
library(quadprog)
solve.QP(Dmat,dvec,Amat,bvec,meq=0,factorized=TRUE)
## $solution
## [1] 2 4 # these are the x and y results
##
## $value
## -587.9768
##
## and some more results...
问题:
- 为什么两个结果不同?
- 我在哪些解法中犯了错误?可以指出来吗?
- 当我从结果中输入 x 和 y 时,我没有得到
solve.QP()替代项的$value- 做数学题时
- 如您所见,结果并不一致
- 我是不是搞错了?!
- 做数学题时
非常感谢!
问题在于
- 问题使用的是 factorized=TRUE
- 问题顶部的 objective 函数暗示 dvec[1] 与问题代码中显示的不同。
如果我们省略分解(默认为 FALSE)并始终使用问题中定义 Dmat、dvec、Amat 和 bvec 的代码,那么我们从 solve.QP 和手动计算 objective 基于解向量,均为-297。 ###### 之前的代码是从问题中逐字复制的。
# Parameters of the objective funtion and the constraints
D=matrix(c(5,7,7,10),ncol=2,byrow=TRUE)
d=c(-78,-108)
A=matrix(c(1,2,1,1),ncol=2,byrow=TRUE)
b=c(10,6)
# Convert the parameters to an appropriate state of solve.QP()
Dmat=2*D
dvec=-d
Amat=-t(A)
bvec=-b
######
library(quadprog)
ans <- solve.QP(Dmat,dvec,Amat,bvec)
str(ans)
## List of 6
## $ solution : num [1:2] 3 3
## $ value : num -297
## ...snip...
# manual calculation of objective function
t(ans$solution) %*% Dmat %*% ans$solution / 2 - dvec %*% ans$solution
## [,1]
## [1,] -297
# another manual calculation - coefficients come from Dmat and dvec
f <- function(x, y) (10 * x^2 + 2 * 14 * x * y + 20 * y^2) / 2 - (78 * x + 108 * y)
f(3, 3)
## [1] -297