计算单个平面上多个标记的单应性
Calculating homography of multiple markers on a single plane
我有一个算法可以计算单个图像中多个标记的单应性，使用 OpenCV 的 findHomography。这工作正常，但由于图像 markers/resolution 的大小，计算的旋转通常非常不准确（主要围绕标记的 x 和 z 轴，假设 y 向上）。我很想找到一种方法来改进它。
我有一个假设，我知道所有标记都在同一平面上（它们在 table 上）应该有助于改善单应性 - 然后我只需要计算出旋转围绕单个轴的标记 - 但我不知道如何将其付诸实践。谁能给我任何指导？
这是我正在尝试处理的情况的示例（标记上的图像与现实中的图像不同）。
单应性模型假设您的标记在一个平面上。这不是您可以添加的附加信息。如果您的标记是 而不是 并且是平面，则该功能将根本不起作用。
如果你的标记都在图像平面内，即所有图像都是俯视图图像，那么你可以使用仿射模型（或更低）而不是单应性模型。从你的问题中不清楚是否是这种情况。
如果你所有的标记总是在同一个平面上，你可以根据所有标记同时计算平面单应性。您拥有的点越多，跨越图像的点越多，结果在数值上应该越稳定。它应该比独立计算每个标记的单应性更准确。
问题是你的对应点是什么——你还需要知道图像中标记的相对位置。
如果您使用相同的参考标记图像，计算很可能会失败。
我喜欢通过使用分布在场景中的多个标记图像来获得更高精度的估计单应性的想法。
这种方法可以使用非线性优化来实现。但这有点棘手。
假设、模型、数据
让我们以放置在 table 上的 3 个打印标记图像为例，并假设您的所有假设都成立。
现在假设对于 3 个打印标记图像中的每一个，您都找到了 N 点对应关系 。
此处的点对应意味着对于打印的标记图像，您可以将 N 图像 像素位置 与相应的 N 现实世界相关联positions (x,y) 相对于已知现实世界 "printed marker coordinate system" 的厘米（或其他单位）（例如，坐标 (0,0) 位于标记图像的中心).
问题是 "printed marker coordinate system" 对于每个打印的标记图像仅在本地已知。我们需要的是将这些坐标系整合在一起，并找到一种方法来在单个全局坐标系中表达 "printed marker coordinate system" 位置。所以我们需要弄清楚它们之间的关系。
每个标记的同形异义关系
我们想要计算单应性，它使用来自不同印刷标记图像的所有对应数据。因此，了解它们之间的关系很重要。具体来说，我们想为所有标记图像找到一个共同的坐标系，以便制定一个优化问题。
现在，根据点的对应关系，用常规的方法，计算出3个单应性：
H1 将标记图像 #1 的 "printed marker coordinate system" 位置映射到图像像素坐标 H2 将标记图像 #2 的 "printed marker coordinate system" 位置映射到图像像素坐标 H3 将标记图像 #3 的 "printed marker coordinate system" 位置映射到图像像素坐标
让我们假设不存在任何测量和计算错误（只是假设）。然后，单应性仅在相应 "printed marker coordinate systems" 的旋转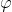 
和平移  "(t_x,t_y)")
上有所不同。
那么，下面的等式成立：
%7D,&space;t_%7Bx%7D%5E%7B(2)%7D,&space;t_%7By%7D%5E%7B(2)%7D) "H_1 &= H_2 \cdot A(\varphi^{(2)}, t_{x}^{(2)}, t_{y}^{(2)})")
%7D,&space;t_%7Bx%7D%5E%7B(3)%7D,&space;t_%7By%7D%5E%7B(3)%7D) "H_1 &= H_3 \cdot A(\varphi^{(3)}, t_{x}^{(3)}, t_{y}^{(3)})")
旋转和平移定义如下：
&space;:=&space;%5Cbegin%7Bpmatrix%7D%5Ccos(%5Cvarphi)&-%5Csin(%5Cvarphi)&t_x%5C%5C%5Csin(%5Cvarphi)&%5Ccos(%5Cvarphi)&t_y%5C%5C0&0&1%5Cend%7Bpmatrix%7D "A(\varphi, t_x, t_y) := \begin{pmatrix}\cos(\varphi)&-\sin(\varphi)&t_x\\sin(\varphi)&\cos(\varphi)&t_y\0&0&1\end{pmatrix}")
把所有东西放在一起
这意味着H1等于H2"up to"一个旋转%7D "\varphi")
和平移%7D,t_y%5E%7B(2)%7D) "(t_x^{(2)},t_y^{(2)})")
并且H1等于H3"up to"一个旋转%7D "\varphi")
和平移%7D,t_y%5E%7B(3)%7D) "(t_x^{(3)},t_y^{(3)})")
.
这为我们提供了一种将标记图像 #2 的位置转换为标记图像 #1 的坐标系的方法（标记图像 #3 的位置可以类似处理）：
%7D%5C%5Cy%5E%7B(1)%7D&space;%5Cend%7Bpmatrix%7D:=%5Cbegin%7Bpmatrix%7D%5Ccos(%5Cvarphi%5E%7B(2)%7D)&-%5Csin(%5Cvarphi%5E%7B(2)%7D)%5C%5C%5Csin(%5Cvarphi%5E%7B(2)%7D)&%5Ccos(%5Cvarphi%5E%7B(2)%7D)%5C%5C&space;%5Cend%7Bpmatrix%7D%5Ccdot%5Cbegin%7Bpmatrix%7Dx%5E%7B(2)%7D%5C%5Cy%5E%7B(2)%7D&space;%5Cend%7Bpmatrix%7D&space;+&space;%5Cbegin%7Bpmatrix%7Dt_x%5E%7B(2)%7D%5C%5Ct_y%5E%7B(2)%7D&space;%5Cend%7Bpmatrix%7D "\begin{pmatrix}x^{(1)}\y^{(1)} \end{pmatrix}:=\begin{pmatrix}\cos(\varphi^{(2)})&-\sin(\varphi^{(2)})\\sin(\varphi^{(2)})&\cos(\varphi^{(2)})\ \end{pmatrix}\cdot\begin{pmatrix}x^{(2)}\y^{(2)} \end{pmatrix} + \begin{pmatrix}t_x^{(2)}\t_y^{(2)} \end{pmatrix}")
现在，在现实世界中，这些方程式将仅近似成立。但是尽管如此，它们还是为估计任何一对印刷标记图像之间的旋转和平移提供了动力：
%7D)&-%5Csin(%5Cvarphi%5E%7B(2)%7D)&t_x%5E%7B(2)%7D%5C%5C%5Csin(%5Cvarphi%5E%7B(2)%7D)&%5Ccos(%5Cvarphi%5E%7B(2)%7D)&t_y%5E%7B(2)%7D%5C%5C0&0&1%5Cend%7Bpmatrix%7D "H_2^{-1}H_1\approx \begin{pmatrix}\cos(\varphi^{(2)})&-\sin(\varphi^{(2)})&t_x^{(2)}\\sin(\varphi^{(2)})&\cos(\varphi^{(2)})&t_y^{(2)}\0&0&1\end{pmatrix}")
%7D)&-%5Csin(%5Cvarphi%5E%7B(3)%7D)&t_x%5E%7B(3)%7D%5C%5C%5Csin(%5Cvarphi%5E%7B(3)%7D)&%5Ccos(%5Cvarphi%5E%7B(3)%7D)&t_y%5E%7B(3)%7D%5C%5C0&0&1%5Cend%7Bpmatrix%7D "H_3^{-1}H_1\approx \begin{pmatrix}\cos(\varphi^{(3)})&-\sin(\varphi^{(3)})&t_x^{(3)}\\sin(\varphi^{(3)})&\cos(\varphi^{(3)})&t_y^{(3)}\0&0&1\end{pmatrix}")
现在，使用 atan2，我们可以找到六个辅助变量的估计值 %7D,t_x%5E%7B(2)%7D,t_y%5E%7B(2)%7D,%5Cvarphi%5E%7B(3)%7D,t_x%5E%7B(3)%7D,t_y%5E%7B(3)%7D) "(\varphi^{(2)},t_x^{(2)},t_y^{(2)},\varphi^{(3)},t_x^{(3)},t_y^{(3)})")
，它们描述印刷标记图像 #2 和 #3 相对于 #1 的位置。
这就是我们准备拥有起始值和模型来制定非线性优化问题所需的全部。
非线性优化问题
最终目标是找到单应矩阵的 8 个系数 H，它同时使用所有打印标记图像的所有点对应关系：
利用上述模型，我们可以定义一个非线性方程组。它将有 8 + 6 个未知数：
- 8个单应系数
- 6 个辅助变量 描述了标记图像#2 和#3 的对应关系如何映射到标记图像#1 坐标系
利用3张标记图像的N个点对应关系，得到N*3*2 = N*6个方程。这意味着，我们需要 N>=3 点对应才能拥有比未知数更多的方程式。有趣的是，在多标记图像场景的情况下，每个标记图像的最小 N=3 对应小于单个标记图像场景的最小 N=4。
我现在不会更详细地添加非线性优化问题的公式，因为已经解释了如何解决该问题的一般思路。
求解非线性优化问题，例如可以使用Newton’s method。
备注
上述等式中的所有矩阵都需要按如下方式归一化：
我同意，为了采用基于点对应的标准单应性估计方法，用户必须知道标记在世界中的相对位置。然而，有一种方法可以改进单应性估计过程。在 this 论文 基于多组点对应关系的单应性排名 中，有一种方法可以系统地推荐在与如上所述。
此外，作者还记录了将任务表述为非线性优化问题的尝试。在补充部分中，有与此问题相关的讨论。长话短说，它表明要获得可用的结果非常困难。我之所以提到这一点，是因为之前的一个答案暗示了这一点。
免责声明：我是上述论文的主要作者。在我的 Ph.D 期间，当我在现实世界的应用程序中遇到完全相同的问题时，我想到了解决方案。研究。
我有一个算法可以计算单个图像中多个标记的单应性，使用 OpenCV 的 findHomography。这工作正常，但由于图像 markers/resolution 的大小，计算的旋转通常非常不准确（主要围绕标记的 x 和 z 轴，假设 y 向上）。我很想找到一种方法来改进它。
我有一个假设，我知道所有标记都在同一平面上（它们在 table 上）应该有助于改善单应性 - 然后我只需要计算出旋转围绕单个轴的标记 - 但我不知道如何将其付诸实践。谁能给我任何指导？
这是我正在尝试处理的情况的示例（标记上的图像与现实中的图像不同）。
单应性模型假设您的标记在一个平面上。这不是您可以添加的附加信息。如果您的标记是 而不是 并且是平面，则该功能将根本不起作用。
如果你的标记都在图像平面内，即所有图像都是俯视图图像，那么你可以使用仿射模型（或更低）而不是单应性模型。从你的问题中不清楚是否是这种情况。
如果你所有的标记总是在同一个平面上，你可以根据所有标记同时计算平面单应性。您拥有的点越多，跨越图像的点越多，结果在数值上应该越稳定。它应该比独立计算每个标记的单应性更准确。
问题是你的对应点是什么——你还需要知道图像中标记的相对位置。
如果您使用相同的参考标记图像，计算很可能会失败。
我喜欢通过使用分布在场景中的多个标记图像来获得更高精度的估计单应性的想法。
这种方法可以使用非线性优化来实现。但这有点棘手。
假设、模型、数据
让我们以放置在 table 上的 3 个打印标记图像为例，并假设您的所有假设都成立。
现在假设对于 3 个打印标记图像中的每一个，您都找到了 N 点对应关系 。
此处的点对应意味着对于打印的标记图像，您可以将 N 图像 像素位置 与相应的 N 现实世界相关联positions (x,y) 相对于已知现实世界 "printed marker coordinate system" 的厘米（或其他单位）（例如，坐标 (0,0) 位于标记图像的中心).
问题是 "printed marker coordinate system" 对于每个打印的标记图像仅在本地已知。我们需要的是将这些坐标系整合在一起，并找到一种方法来在单个全局坐标系中表达 "printed marker coordinate system" 位置。所以我们需要弄清楚它们之间的关系。
每个标记的同形异义关系
我们想要计算单应性，它使用来自不同印刷标记图像的所有对应数据。因此，了解它们之间的关系很重要。具体来说，我们想为所有标记图像找到一个共同的坐标系，以便制定一个优化问题。
现在，根据点的对应关系，用常规的方法，计算出3个单应性：
H1将标记图像 #1 的 "printed marker coordinate system" 位置映射到图像像素坐标H2将标记图像 #2 的 "printed marker coordinate system" 位置映射到图像像素坐标H3将标记图像 #3 的 "printed marker coordinate system" 位置映射到图像像素坐标
让我们假设不存在任何测量和计算错误（只是假设）。然后，单应性仅在相应 "printed marker coordinate systems" 的旋转 和平移
上有所不同。
那么，下面的等式成立：
旋转和平移定义如下：
把所有东西放在一起
这意味着H1等于H2"up to"一个旋转和平移
并且H1等于H3"up to"一个旋转
和平移
.
这为我们提供了一种将标记图像 #2 的位置转换为标记图像 #1 的坐标系的方法（标记图像 #3 的位置可以类似处理）：
现在，在现实世界中，这些方程式将仅近似成立。但是尽管如此，它们还是为估计任何一对印刷标记图像之间的旋转和平移提供了动力：
现在，使用 atan2，我们可以找到六个辅助变量的估计值 ，它们描述印刷标记图像 #2 和 #3 相对于 #1 的位置。
这就是我们准备拥有起始值和模型来制定非线性优化问题所需的全部。
非线性优化问题
最终目标是找到单应矩阵的 8 个系数 H，它同时使用所有打印标记图像的所有点对应关系：
利用上述模型，我们可以定义一个非线性方程组。它将有 8 + 6 个未知数：
- 8个单应系数
- 6 个辅助变量
利用3张标记图像的N个点对应关系，得到N*3*2 = N*6个方程。这意味着，我们需要 N>=3 点对应才能拥有比未知数更多的方程式。有趣的是，在多标记图像场景的情况下，每个标记图像的最小 N=3 对应小于单个标记图像场景的最小 N=4。
我现在不会更详细地添加非线性优化问题的公式，因为已经解释了如何解决该问题的一般思路。
求解非线性优化问题，例如可以使用Newton’s method。
备注
上述等式中的所有矩阵都需要按如下方式归一化：
我同意，为了采用基于点对应的标准单应性估计方法，用户必须知道标记在世界中的相对位置。然而，有一种方法可以改进单应性估计过程。在 this 论文 基于多组点对应关系的单应性排名 中，有一种方法可以系统地推荐在与如上所述。
此外，作者还记录了将任务表述为非线性优化问题的尝试。在补充部分中，有与此问题相关的讨论。长话短说，它表明要获得可用的结果非常困难。我之所以提到这一点，是因为之前的一个答案暗示了这一点。
免责声明：我是上述论文的主要作者。在我的 Ph.D 期间，当我在现实世界的应用程序中遇到完全相同的问题时，我想到了解决方案。研究。