Tail-call 递归方程的优化
Tail-call optimization in recursive equations
我有以下两个相互递归的函数,
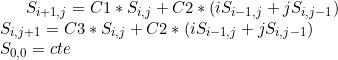
由于 Python 不能很好地处理 tail-call 优化,程序员应该将这些函数表示为有状态循环。 Python 社区使用什么技术将这种方程式转换为显式循环?
或者这些变换algorithm-dependent和每个递归函数必须单独分析?
递归实现:
让C1 = xpa, C2 = p and C3 = xpb然后
def obaraSaika(p,s00x,i,j,xpa,xpb):
if i < 0 or j < 0: return 0
if i == 0 and j == 0: return s00x
if i >= 1: return xpa*(obaraSaika(p,s00x,i-1,j,xpa,xpb)) + \
p*((i-1)*(obaraSaika(p,s00x,i-2,j)) + j*(obaraSaika(p,s00x,i-1,j-1,xpa,xpb) ) )
if j >= 1: return xpb*(obaraSaika(p,s00x,i-1,j,xpa,xpb)) + \
p*(i * (obaraSaika(p,s00x,i-1,j-1)) + (j-1)*(obaraSaika(p,s00x,i,j-2,xpa,xpb) ) )
这个实现的想法是先使用i索引遍历树,然后i == 0一次,使用j索引减少树。
将任何递归算法转换为等效的非递归算法都很简单。
执行递归调用时,实际上是将一组参数压入堆栈。此堆栈由 Python 解释器提供给您。
所以,不用递归重写算法的方法是……你自己管理堆栈!当您进行递归调用时,您取而代之的是获取您将传递的所有参数并将它们推送到您的堆栈对象上。然后你有一个 "driver" 循环,它反复从堆栈中弹出并执行其中列出的计算。
这类程序的特征是有一个堆栈对象,您可以用初始状态 tuple/object 为它初始化,然后是一个 while len(stack) > 0 循环,一直运行到您完成为止。
您基本上只是做递归会做的事情,但是当您自己管理相关数据结构时,它会为您提供更好的提高效率的机会。
这种特殊类型的转换适用于任何算法。其他的,特别是那些涉及在对相关函数的不同调用之间携带全局状态的,是依赖于算法的。
我有以下两个相互递归的函数,
由于 Python 不能很好地处理 tail-call 优化,程序员应该将这些函数表示为有状态循环。 Python 社区使用什么技术将这种方程式转换为显式循环?
或者这些变换algorithm-dependent和每个递归函数必须单独分析?
递归实现:
让C1 = xpa, C2 = p and C3 = xpb然后
def obaraSaika(p,s00x,i,j,xpa,xpb):
if i < 0 or j < 0: return 0
if i == 0 and j == 0: return s00x
if i >= 1: return xpa*(obaraSaika(p,s00x,i-1,j,xpa,xpb)) + \
p*((i-1)*(obaraSaika(p,s00x,i-2,j)) + j*(obaraSaika(p,s00x,i-1,j-1,xpa,xpb) ) )
if j >= 1: return xpb*(obaraSaika(p,s00x,i-1,j,xpa,xpb)) + \
p*(i * (obaraSaika(p,s00x,i-1,j-1)) + (j-1)*(obaraSaika(p,s00x,i,j-2,xpa,xpb) ) )
这个实现的想法是先使用i索引遍历树,然后i == 0一次,使用j索引减少树。
将任何递归算法转换为等效的非递归算法都很简单。
执行递归调用时,实际上是将一组参数压入堆栈。此堆栈由 Python 解释器提供给您。
所以,不用递归重写算法的方法是……你自己管理堆栈!当您进行递归调用时,您取而代之的是获取您将传递的所有参数并将它们推送到您的堆栈对象上。然后你有一个 "driver" 循环,它反复从堆栈中弹出并执行其中列出的计算。
这类程序的特征是有一个堆栈对象,您可以用初始状态 tuple/object 为它初始化,然后是一个 while len(stack) > 0 循环,一直运行到您完成为止。
您基本上只是做递归会做的事情,但是当您自己管理相关数据结构时,它会为您提供更好的提高效率的机会。
这种特殊类型的转换适用于任何算法。其他的,特别是那些涉及在对相关函数的不同调用之间携带全局状态的,是依赖于算法的。